モンテカルロ・シミュレーション＝自由なサイコロを何回も投げる

自由なサイコロとは？値はなんでもよい？

モンテカルロ・シミュレーションとは「自由に設定されたサイコロを何度も投げる」プロセスです。

「サイコロは1～6までの値が出る6面の立方体じゃないの？」と思われるかもしれません。 もしくは、近年バラエティ番組でよく見かける20面のサイコロも考えられます。

もし自由に面の数や出現する値をいじることができたらどうでしょうか？ 例えば、レストランを経営している人が、
　・その日の来客数を占ってくれる
　・そのお客さんの平均支払額を教えてくれる
という2つのサイコロを持ってれば、オープン前にその2つの「自由なサイコロ」を投げて その日のおおよその売上を占うことができます。

このレストランの経営者がやっていることが、「モンテカルロ・シミュレーション」そのものです。 その日の来客数を占ってくれるサイコロとそのお客さんの平均支払額を教えてくれるサイコロを、 1回だけでなく100回投げれば、100日分の売上を占ってくれます。

モンテカルロ・シミュレーションで「明日」や「1年間」を次々と生み出す

レストランの明日の売上以外にも、世の中には簡単には予測できないこと数多く存在します。 企業の翌年1年間の売上や経費、翌日の株価、商品が売れる個数、1分間にかかって来る電話の回数など、 身の回りのことを考えると簡単に思いつくことができるかと思います。

確かに、ピタリとその値を当てることはほぼ不可能ですが、 「なんとなくこんなことが起こりそう」であれば、誰でも考えることができます。 ただし、大雑把すぎると誰もその予測を信頼してくれません。

そこで、先ほどのレストランの例のように、サイコロが明日を占ってくれる状況はどうでしょうか。「サイコロを100回投げた結果から、平均的にこんなことが起こりそうです」であれば、 少しは説得力が上がるかもしれません。

なぜなら、サイコロを100回投げた＝100日分営業したと言えるからです。 仮想的に100日営業した結果から予測をすれば、ピタリと当たらないまでも説得力があります。

自由なサイコロの作り方（モンテカルロ・シミュレーションの下準備）

サイコロを表す図形：確率分布という考え方

レストランの「その日の来客数を占ってくれる」サイコロは、 １～6までの値が出現する一般的なサイコロではなく、 いろいろな来客数が面に書かれているサイコロでなければなりません。

さらに、これまでの経験で「だいたいこれくらいの来客数だろう」ということがわかっているとすれば、 その値に近い値（サイコロの目）はなるべく多く出る、反対にそこから外れた値は少なく出る、 というようになっていないと現実から離れたサイコロを振っていることになってしまいます。

つまり適当にサイコロを作ればいいわけではなく、 起こりやすい値・数値やその範囲を決めてサイコロを作る必要があります。

そこで、起こりやすい値・数値やその範囲を図形を用いて決めてあげます。 例えば、図のような三角形であれば、高さが高いほど出現頻度が高く、 反対に高さが低いほど出現頻度が低いサイコロを表すことにします。 また、左端と右端の値はサイコロの目の最小・最大とみなすことにします。

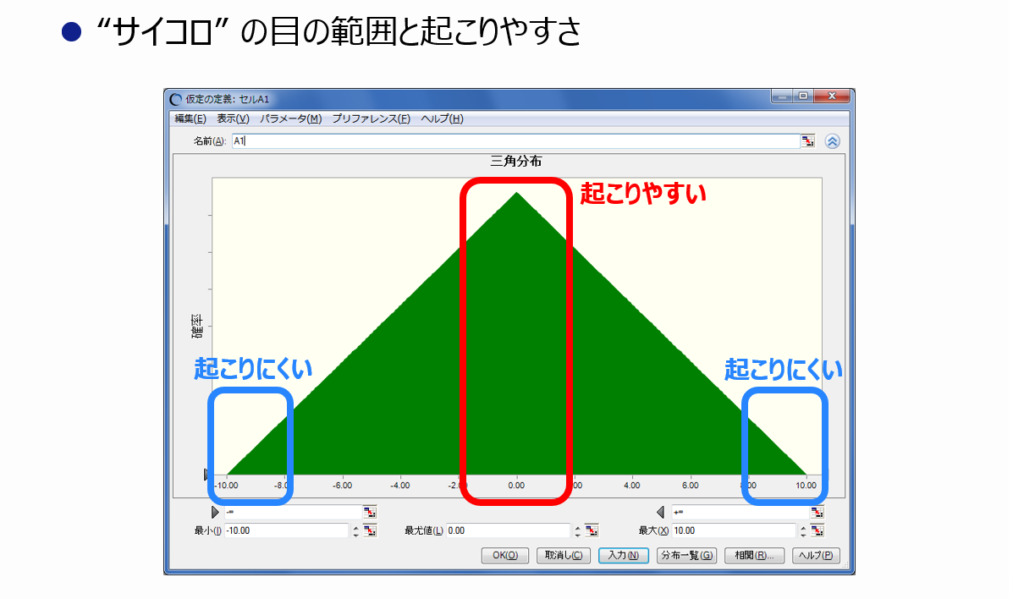
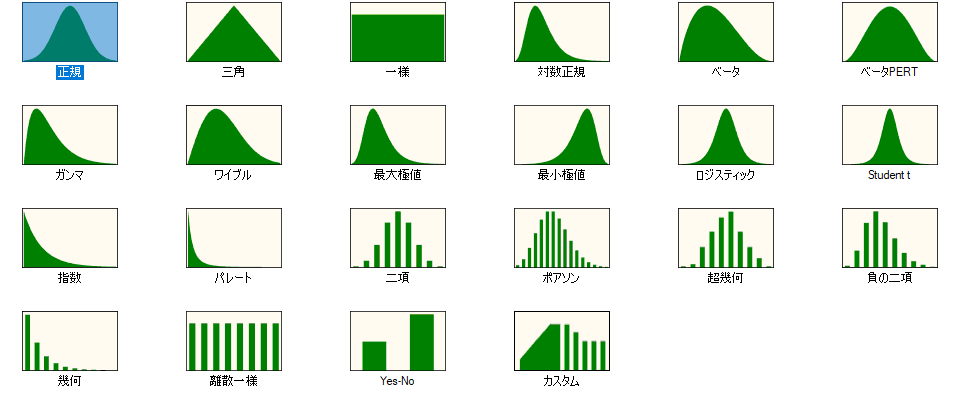
このサイコロの値と起こりやすさを決める図形のことを確率分布と呼びます。 確率分布は三角形（三角分布）や長方形（一様分布）以外にも、釣り鐘型（正規分布）をはじめ様々な分布が存在します。いくつかご紹介いたします。

三角分布

最小、最大、最頻（もっとも起こりやすい）の３点を定義する分布となります。シンプルで直感的、分かりやすいためよく利用されます。特に経験的に設定する場合やデータが少ない場合に適します。

一様分布

最小、最大のみで定義される、すべての値が同じ確率で発生する分布となります。すべての結果が等しく起こりうる場合に使用されます。経験的に幅でしかわからないようなケースや、乱数生成などに利用されます。

正規分布

平均値と標準偏差（ばらつき具合）で定義される、左右対称の分布となります。自然現象や人間の特性など多くのデータがこの正規分布に従うとされており、その分の説明性があります。

対数正規分布

対数が正規分布に従う分布となります。すべて正の値を取り、右に長い尾を持ち、特に金融データなどでよく利用されます。（Crystal Ball では０以外の場所から始まるように設定できます）

Yes-No分布（Crystal Ball の名称）

0 か 1 のみを表す分布となります。0が30%、1が70% といった設定が可能です。非常にシンプルですが、発生確率や成功確率といった、起こる／起こらないという現象を簡単に表現することが可能です。

サイコロを「作って投げる」はコンピュータに任せる（モンテカルロ・シミュレーションの実施）

以上より、未来を生み出してくれるサイコロを作り何回も投げることで、おおよその予測ができることがわかりました。 ただし、いざ実践しようとするといくつか問題が出てきます。例えば、

• どうやって自由に設定されたサイコロを用意するか
  （図形とサイコロをリンクさせる方法）
• どうやって何回もサイコロを振るか
  （さすがに10000回も投げるのは・・・）

という点が挙げられます。

「できれば簡単にやりたい」。まさに皆様の声だと思いますが、これをExcel上で可能にしたソフトウェアが「Crystal Ball」です。 「Crystal Ball」を用いると、Excelのセル1つ1つを「自由なサイコロ」として機能させることができます。 また「サイコロを振って未来をたくさん出現させる」といったことも簡単に行うことができます。

Excelを用いて、いろいろな数値計算を行っている方は多いと思いますが、 シナリオを変えるたびに値を手で書き換えるのはとても面倒です。 その作業が「サイコロを振るように」「何回も作ることができる」状態になれば・・・ それでは、一般的にモンテカルロ・シミュレーションはどのように実施するのでしょうか。

モンテカルロ・シミュレーションの実施方法

④シミュレーション

最後にシミュレーションを実施します。確率分布に基づいた乱数が発生して、モデルに沿った計算がなされ、結果が算出されます。この工程を数千回や数万回など繰り返し実施することで、さまざまなケースを洗い出します。こちらがモンテカルロ・シミュレーションの実施手順となります。

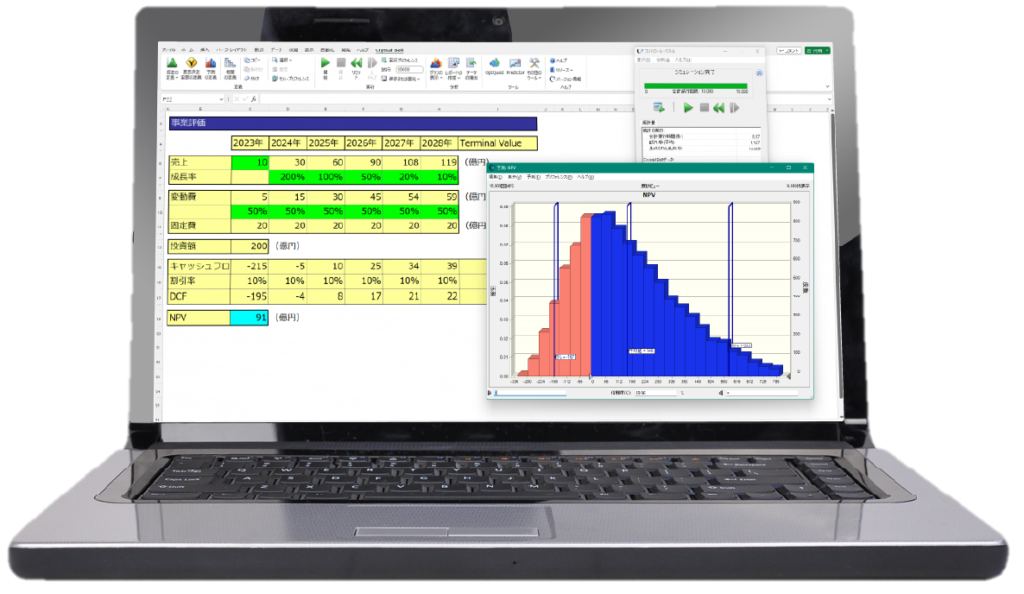
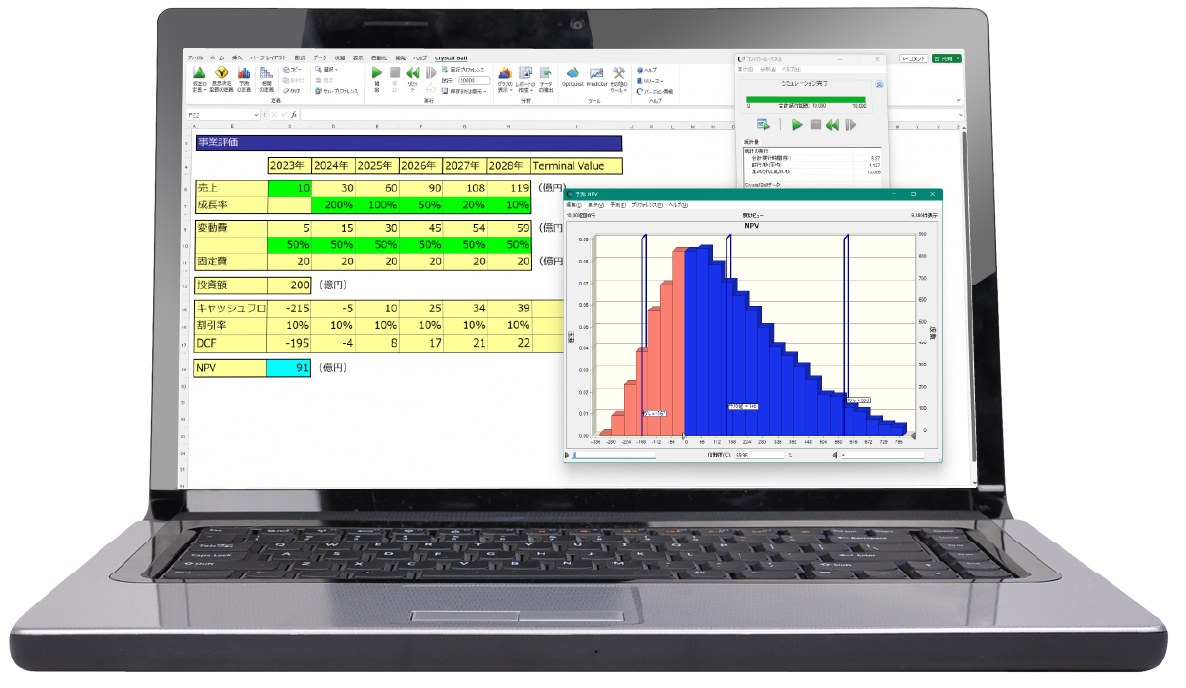
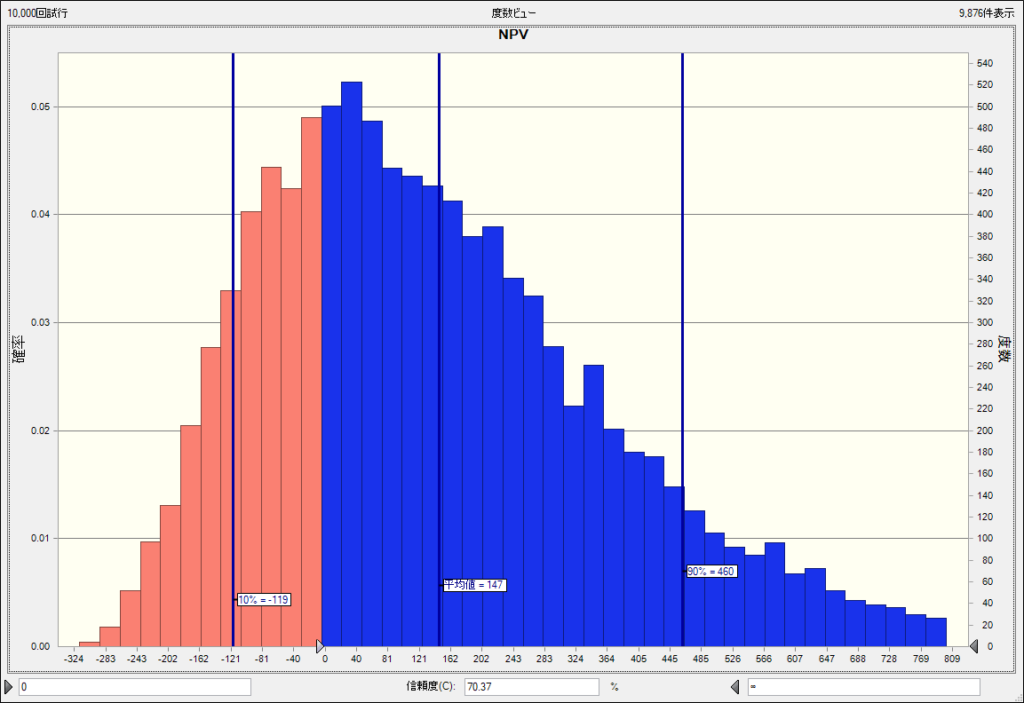
下図はCrystal Ball を活用して実施したモンテカルロ・シミュレーションの結果となります。横軸はNPVという指標、縦軸は、それぞれがどの程度発生したかという頻度・確率になります。山が高くなっているところは起こりやすく、低いところは起こりにくいということになります。例えば以下のような分析が可能です。

• NPVは -300～800ほどのバラつきを持つ、そのうち-119～460 に80%が納まる
• 平均は147程度である
• NPVが0以上となるのは約70%である

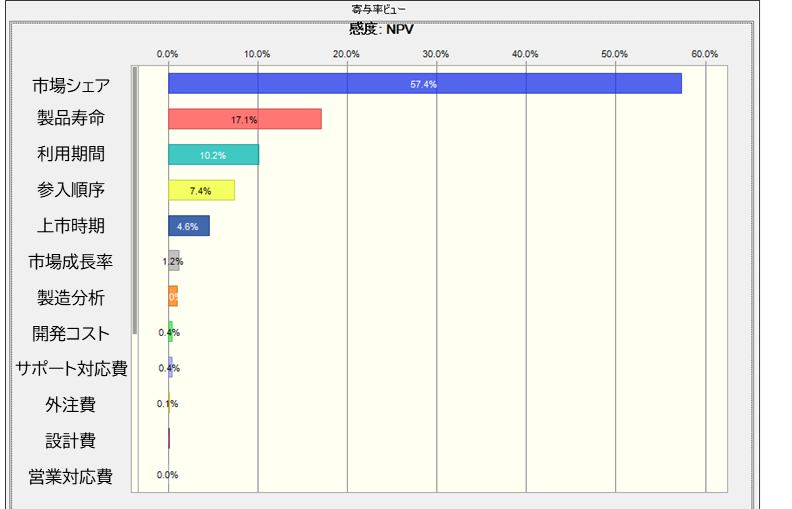
⑤感度分析

モンテカルロ・シミュレーションとセットで用いられる強力な分析となります。結果に対しての影響度を一覧にすることができます。改善策を検討したり、対策の優先順位付けを行うなど、様々に活用することが可能です。

感度分析の活用事例、計算方法などの詳細を知りたいという場合には、こちらの資料ダウンロードかお問い合わせフォームよりお願いいたします。

モンテカルロ・シミュレーションの実施手順まとめ

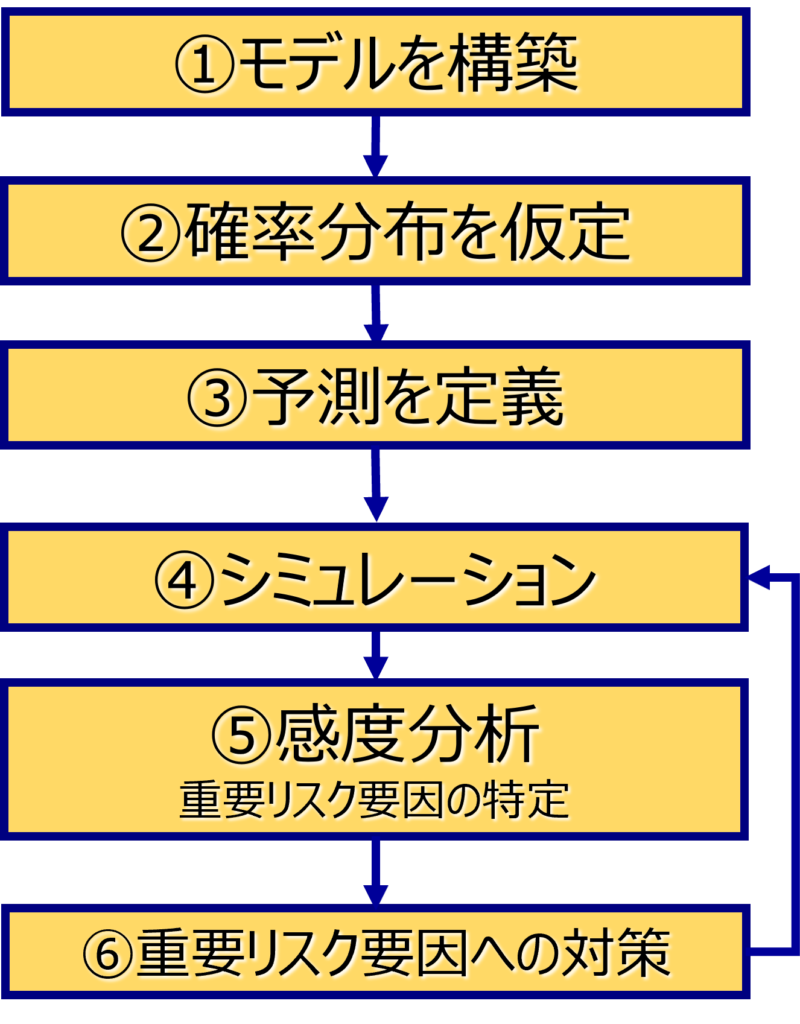
以下に手順をフローとしてまとめております。モンテカルロ・シミュレーションの結果を知りたいという場合には、①～④がその手順となります。

今回⑥については触れておりませんが、リスク分析のためのモンテカルロ・シミュレーションという観点では、リスクを感度分析で特定したあとに、対策を行い、再びモンテカルロ・シミュレーションを実施するというサイクルを回すことが有効とされています。

モンテカルロ・シミュレーションを手軽に実施したい場合：Crystal Ball をご利用ください

上記では Crystal Ball というExcelのアドインを活用して、モンテカルロ・シミュレーションを実施いたしました。

モンテカルロ・シミュレーション自体はExcelの関数を駆使したり、最近ではPythonなどを用いても実施は可能です。しかし、シミュレーションのモデルを何度も変えたり、確率分布を変更したり、シミュレーション結果を分析する際には、手間がかかります。感度分析まで実施する場合にはなおさらとなります。

手軽にモンテカルロ・シミュレーションを実施されたい場合には、Crystal Ball をご活用ください。分析されたいExcel シートを既にお持ちの場合には、数クリックで分析が完了します。以下より試用版（15日間のみ無料体験）をダウンロードいただけます。ぜひお試しください。

モンテカルロ・シミュレーションを活用した事業リスク分析

事業リスク分析とは：ビジネスにおけるリスクをどう取り扱うか

モンテカルロ・シミュレーションの活用例として事業リスク分析が挙げられます。事業性評価や需要予測、売上予測、投資効果の予測、マーケティング関連の分析によく使われています。

モンテカルロ・シミュレーションには、分からないもの・決められていないものをそのままに扱えるというメリットがあります。 例えば、売上や成長率、為替、競合の動き、業界成長率、製品スペックの想定などです。さらに、これらの影響をまとめて確認して、何が重要な因子になっているのかを特定できるというのもポイントです。

ビジネスを取り巻く環境は不確実なものである一方、事業戦略を検討する企画系、製品戦略系、営業マーケ系、管理系などの業種で多く活用されます。 活用目的として、自部門／製品サービス／全社の計画策定・中期経営計画などに載せる業績報告等や、新規事業、研究開発投資、設備投資、ポートフォリオ管理などが多く挙げられます。

以下に、モンテカルロ・シミュレーションを用いた事業リスク分析について、3点のメリットを挙げます。

メリット① 予測の妥当性向上

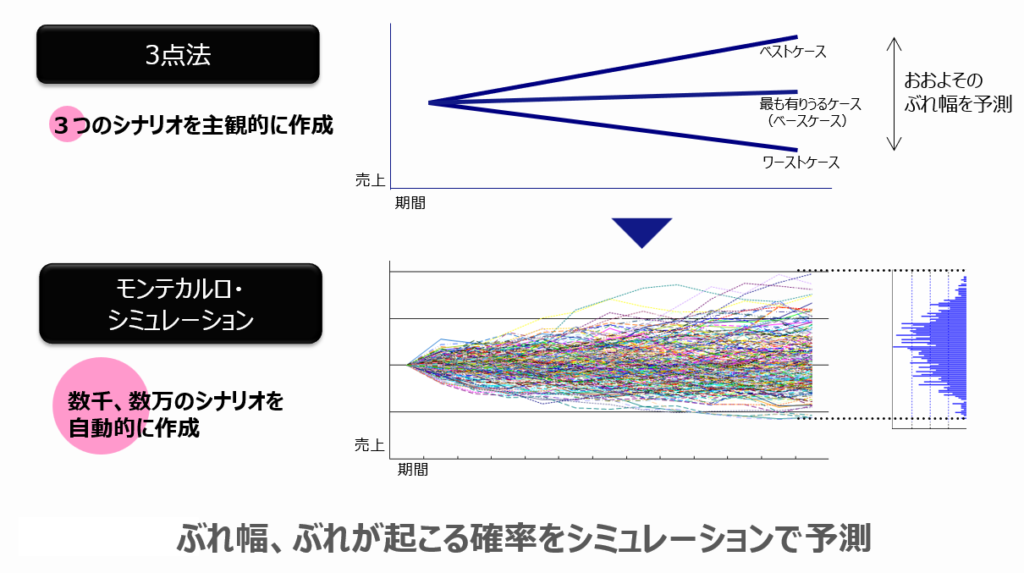
モンテカルロ・シミュレーションを活用することで、様々なリスクや想定を織り込み、より妥当な予測を行います。例えば、良い・普通・悪いの3ケースを確認する場合と比較して、数千・数万のシナリオを発生させることで、予測に関する理解を深化します。これにより、分析前には見えていなかった点を洗い出し、過少・過剰な評価を防ぎます。

さらに、起こりうるケースを網羅的に確認することで、３点法にありがちな評価のばらつきを防ぐことも可能です。施策を打つ際にも、リスク込みで比較することで妥当性を確認することができます。

メリット② リスクの順位付け

感度分析を通じて、評価指標に対してのリスクの影響度を分析できるようになります。分析結果を元にして施策の優先順位付けを行うことが可能です。また、対策すべきリスクに定量的な順位付けがなされることで、担当者が考える施策が有効であることを周囲に示し、施策を進めやすくなります。

メリット③ コミュニケーション／説明性の向上

確率や数値の活用を通じて、客観的で説明性の高い予測に向けた一歩を踏み出すことが可能となります。

同じ状況においても、担当者ごとに予測結果や報告内容にはばらつきが生まれます。幅や確率といった考え方をもって定量的に進めることで、個々人のばらつきが可視化され、コミュニケーションの土壌が生まれます。

モンテカルロ・シミュレーションの業界別活用例

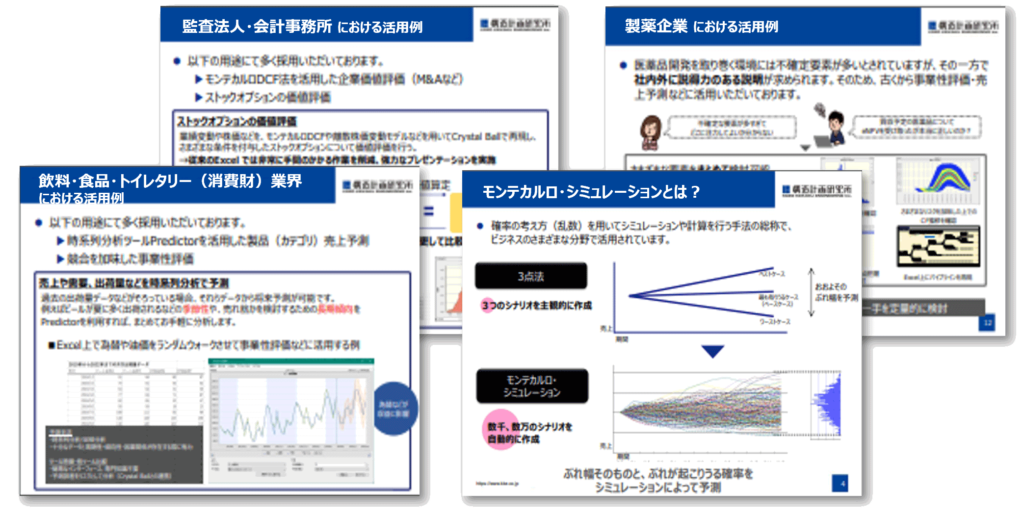
モンテカルロ・シミュレーションを活用しての検討が可能となる業界に制限はありませんが、 メーカー/重工業、製薬/ヘルスケア、資源/インフラ、監査法人/会計事務所、飲料・食品、消費財、保険・再保険、不動産、金融機関、教育（MBA, MOT）…などで特に多く活用されています。

確率的な分析をしたいというシーンについて、以下にいくつか事例を列挙します。詳細な活用例については資料に記載いたします。また、資料にないものや、モンテカルロ・シミュレーションのより具体的な活用につきましてはお問い合わせフォームにて承ります。

製造業

• 製品の売上予測、需要予測
• 新規事業の事業性評価
• ライフサイクルアセスメント
• 安全在庫計算
• 為替リスクのヘッジ

製薬・ヘルスケア

• 新薬パイプラインに関する事業性評価
• 製品の売上予測、需要予測
• 成功確率などを加味したポートフォリオの管理の高度化
• PK/PD解析
• 製品設計の最適化

保険・再保険

• 取り扱い保険のVaR 算出
• キャプティブマネジメント
• 相関などを加味したリスク計算

資源開発・エネルギー関連

• 大型設備投資のROI算出
• 不確実性を加味したサプライチェーン最適化
• プロジェクトのクリティカルパス分析
• 資源埋蔵量評価
• 電力のスポット取引価格予測
• 油価のランダムウォーク計算

会計・監査

• デリバティブ評価
• ストックオプションの公正価値評価
• 株価のランダムウォークを考慮した企業価値評価

エンジニアリング

• プロジェクトマネジメントにおけるクリティカルパス分析、PERT分析
• 製品の成分含有量計算、被ばく量計算
• コンクリートの劣化評価
• 地質分析

金融

• エクスポージャー算出
• 企業価値評価、モンテカルロDCF法の実施
• 解析的な計算が困難な契約／オプションの価値評価
• 相関を考慮したポートフォリオ設計やリスク計測

AIなど他の分析手法との違い：個人や組織の意思決定力を向上

モンテカルロ・シミュレーションは、機械学習やAIとは異なります。それらの手法では過去のデータを用いて将来を見通すアプローチとなります。大量のデータと高度なアルゴリズムを活用し、パターンを見つけて予測を行います。予測結果そのものが価値となります。

一方で、モンテカルロ・シミュレーションは多くの場合、リスクの切り分けや影響度の分析を通じ、人間の意見に客観性や説明性を持たせることでより良い意思決定を目指すという、人間味のあるアプローチとなります。特に事業リスク分析においては、複数のシナリオをシミュレーションすることで将来の不確実性を評価して、よい意思決定を目指します。個人や組織が良い意思決定を考えるように仕向けることが価値となります。

モンテカルロ・シミュレーションの「ヒューレット・パッカード社」における活用例