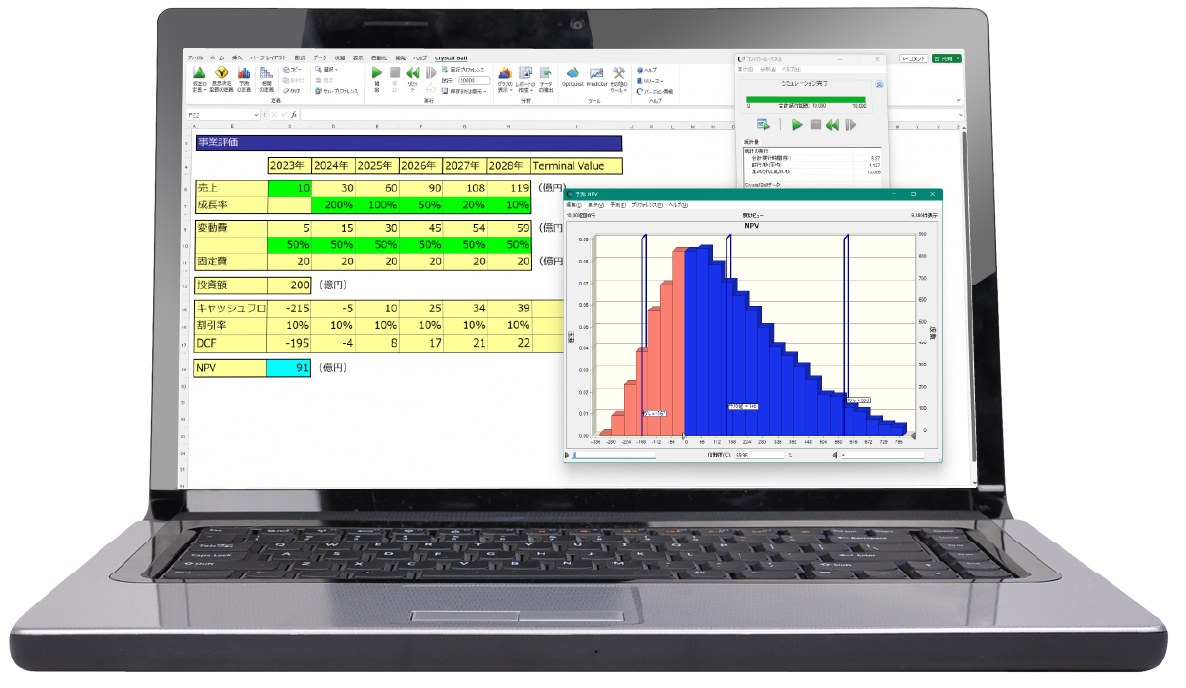
Crystal Ball
最適化
シーンに応じて「最適」が何かは変わっていきますが、いずれにしても計算が難しいことに変わりはありません
最適化とは?
最適化という言葉がありますが、そもそも「最適」とは一体どのようなものでしょうか? 例えば「最適な手法」という言葉を用いるとき、「この手法は最短時間で作業を完了できます」や「最少の人員で済みます」 といった数値的な保証がなされていないと、その手法が最適とは言えません。
このように、「その解は本当に最適なのか?」という問いに答えるための定量的な評価を行うことが必須です。つまり最適化は「定量的に最適性が保証できる解を求めること」なのです。
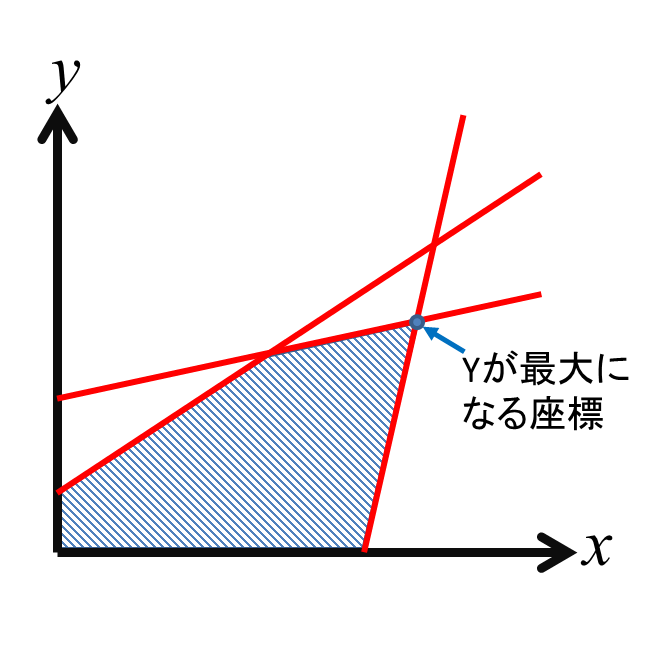
最適化の難しさ
最適化が難しいといわれているのは、解を求めることが困難であるからではありません。 考えられる解の中で「これよりも良い解がない」という保証を得ることが難しいのです。 例えば、図のようにたくさんの都市を一筆書きですべて巡るルートを考えてみてください。 ルートを発見することは非常に簡単ですが、そのルートが最短であることが果たして容易に言えるでしょうか? 理論的にはほぼすべてのルートを探索して長さを比較しないと最短であることが言えません。 都市の数が少ない場合はそこまで時間がかからないかもしれませんが、都市の数が増えればルートの数は莫大になります。 都市の数をnとすればルートの総数はn!(逆回りを同一ルートと考えると(n-1)!/2)通り存在します。 実際にnに大きな数を入れて計算すると、ルートの総数が莫大な数になることがお分かりいただけるかと思います。
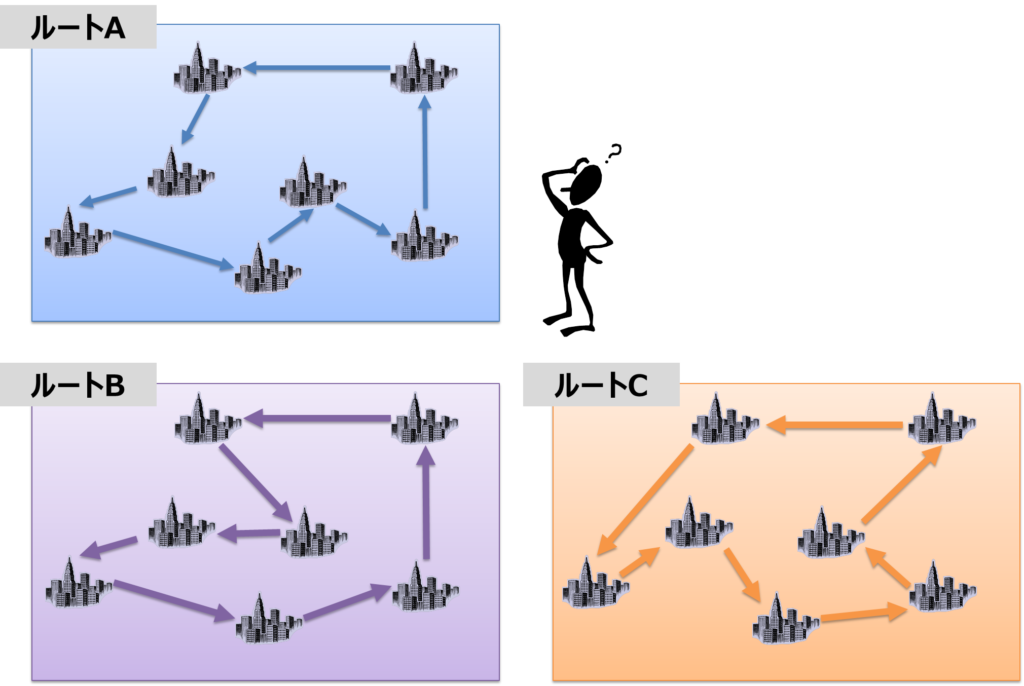
最適化とモンテカルロ・シミュレーション
上の都市を巡る問題を少しアレンジして、距離ではなく時間的に最短なルートを求めることを考えます。 都市間の距離は一般に不変ですが、時間は交通状況や天候によって変化します。 そのような不確実な要因を最適化することは不可能です。なぜならそのルートが最短になる保証が全くないからです。 そこで厳密な最適解ではなく、最適ではないが最適に近い解(近似解)を求めることにします。 つまり「様々な不確実性を考慮する中で平均的に良い解」を求めることを考えるのです。
不確実性を考慮するときに力を発揮するのがモンテカルロ・シミュレーションです。 時々刻々と変化する都市間所要時間を乱数で表現し、様々な状況下でのルート構築を行います。 都市の数が少なければ、10000回シミュレーションを行い平均的に所要時間が最も小さくなるルートを求めることが可能です。 下図はA、B、C、D、Eの5つの都市に対し、時間変動を考慮した最適化を行った様子です。下記の結果は「A→B→D→E→C→A」となりました。
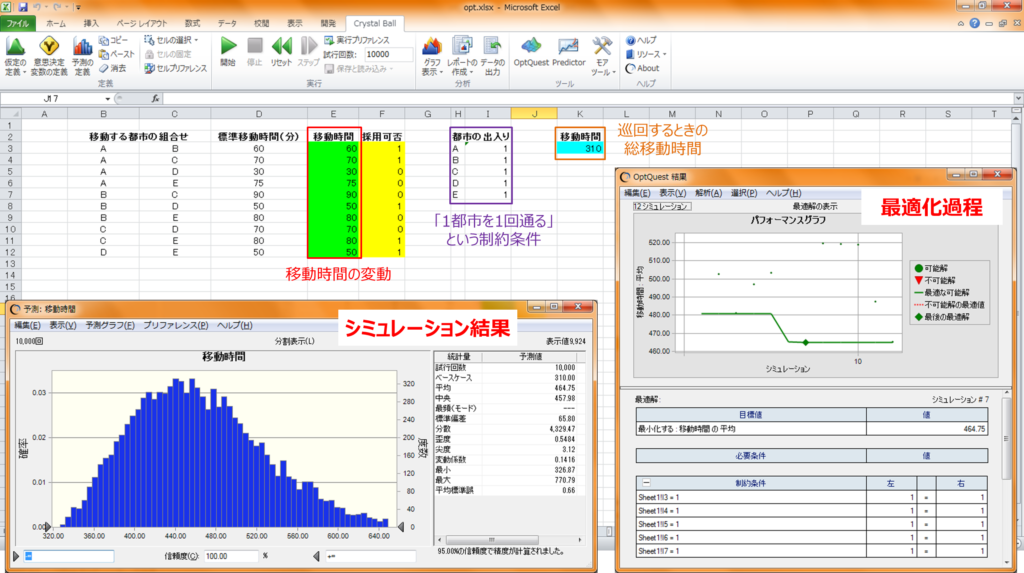
Crystal Ballにおける最適化
今回の例では、世間で広く知られている「都市を一筆書きで巡る問題(巡回セールスマン問題)」を例に最適化を説明してきましたが、 最適化を適用できる事例は数多く存在します。リスクを加味した最適化では、例えば得られるリターンと成功率に幅がある投資案件がいくつかあり、 その中から限られた予算でプロジェクトを選択する場合はモンテカルロ・シミュレーションが非常に有効です。
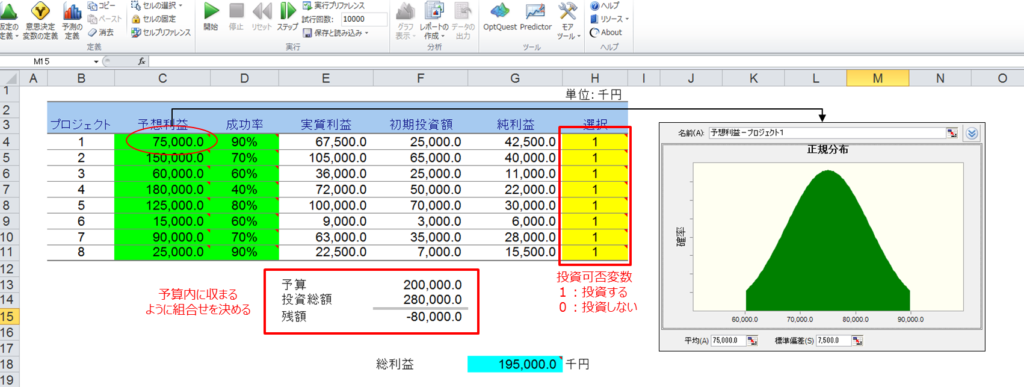
実際に使ってみよう!
Crystal Ballのプロパックにはモンテカルロ・シミュレーションを用いて最適化を行う機能があります(スタンダードにはございません)。この機能もモンテカルロ・シミュレーションと同様にExcel 上で使用することができ、特別なプログラミングをすることなく最適化を行うことができます。 制約条件や必要条件を設定し、あらかじめ探索範囲や求められる解に制限を設けることも可能です。 都市の例でいけば、ある2組の都市間移動に時間的な制約を設けたり、全都市を巡回する時間が1時間以上を超える解は除外するといった設定が考えれます。
さて、Crystal Ball は無料の試用版を下記よりダウンロードできますので、この機会に是非お試し下さい。実際に上記のサンプルについて、各種パラメータや制約条件を変更してみましょう。
また、定期開催のセミナーでは「モンテカルロシミュレーションを活用した最適化」を弊社スタッフ指導の元で体験いただくことも可能です。 Crystal Ballを利用できるPCや、豊富なサンプルファイル、場合によっては弊社cafeのおいしいコーヒーなどもご用意してお待ちしております。是非、参加をご検討ください。
資料ダウンロード

弊社の個人情報に関する取り扱いについては「個人情報の取り扱いについて」(プライバシーマーク付与認定済)をご覧ください。

