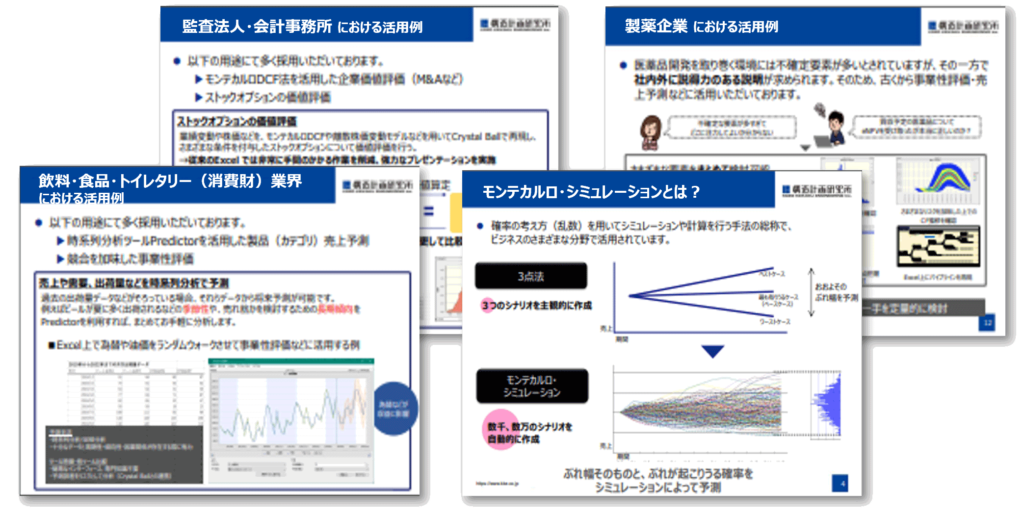
Excelをベースにしたタスク管理!クリティカルパス分析による効率化
特にプロジェクトマネジメントなどでよく活用される手法となります。モンテカルロ・シミュレーションの活用とともにご紹介いたします。
クリティカルパスとは
多様なタスクの積み重ねを分析
タスク管理やプロジェクトマネジメントで最も重要な要素のひとつがクリティカルパスを把握することです。 工程の作成には経験やノウハウだけでは対応できない不確実な要因が含まれる場合があります。 こういった不確実性を加味した上でどの程度の確率で工程に影響がでるかを 計画段階で把握することでタスクの遅延による莫大な損害を防ぐことができ、その後の工程のスケジューリングにも役立ちます。
あるプロジェクトが、タスクの複雑な積み重ねで構成されるとお考え下さい。グラタンを振舞うには、いつどこで料理するかを決めて、レシピを決め、買い出しに行き、じゃがいもを洗い、スライスし、ソースを並行して作り、すべての具材が合わさった状態でオーブンにかけます。Uber Eatsや出前館を使わずに最も早く完了するには、事前にどのような手順で料理するかを考える必要があります。
クリティカルパスとは、そのプロジェクトを最短で完了するための、タスクの消化順序を指します。
今回はExcelをベースにしたタスク管理と題して、 Excelへのアドインが可能なリスク分析ツール Crystal Ball を用いて不確実な要因を考慮した クリティカルパス分析を行い、工程への影響度が大きいタスクを改善した場合の効果を分析した事例をご紹介します。
キーワード: PERT法、工程管理、クリティカルパス、スケジューリング
クリティカルパスをモンテカルロ・シミュレーションで検討
PERT図を作成してシミュレーションで把握
タスク管理では工程に番号を付け流れを把握するPERT図を作成し各タスクの活動時間を計算します。
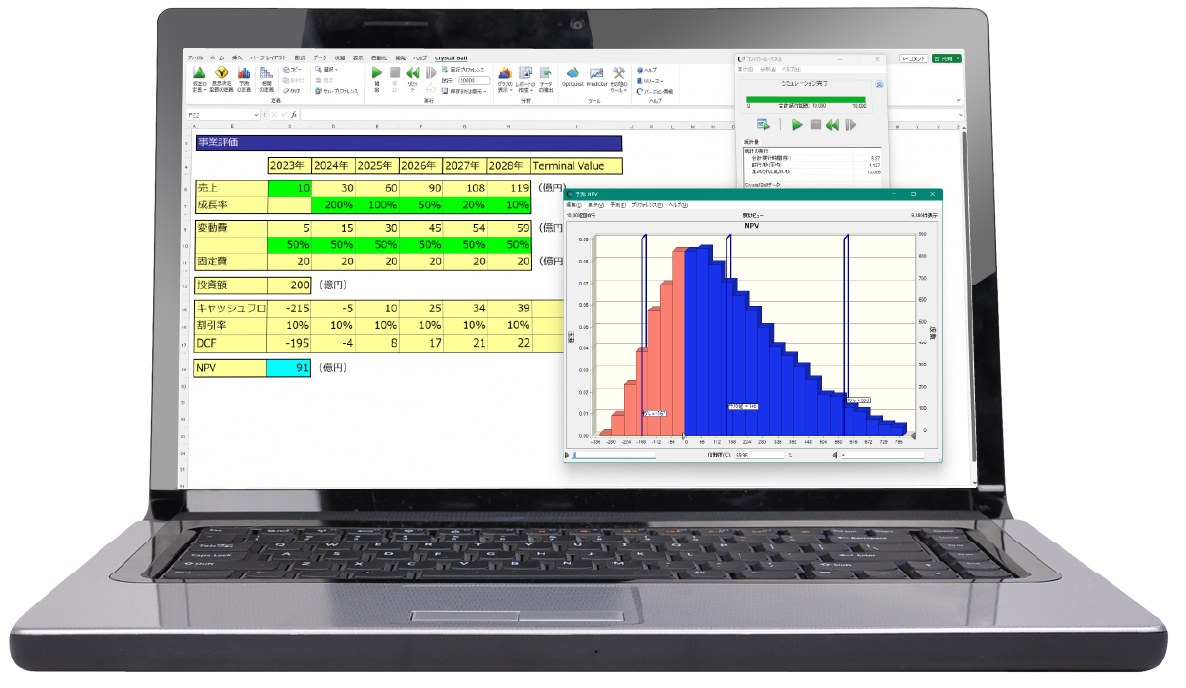
本タスク管理ではタスク5,10,11のように複数のタスクが完了しないと開始できないものがあるためタスクの相互関係を踏まえたモデルをExcelのスプレッドシート上に作成します。例えばタスク5はタスク3,4の完了後に開始されるため開始時間はタスク3の終了時刻である8:00と設定されております。各タスクの活動時間は変動する不確実な要因であるため確率分布(最小値、最尤値、最大値からなる三角分布)として定義し、 試行回数10,000回のモンテカルロ・シミュレーションによりプロジェクト完了時間を確率的に分析します。なお、本検討ではプロジェクト完了時間の目標値は21時間と設定しております。
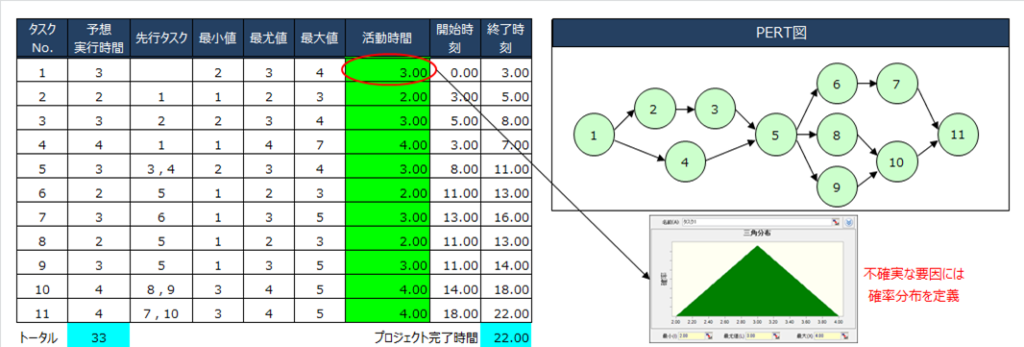
今回は確率分布として三角分布を利用していますが、Crystal Ball はこの手のシミュレーションでよく使われる「ベータPERT分布」もご利用いただけます。
感度分析でクリティカルパスを確率的に把握
改善施策の定量比較も可能
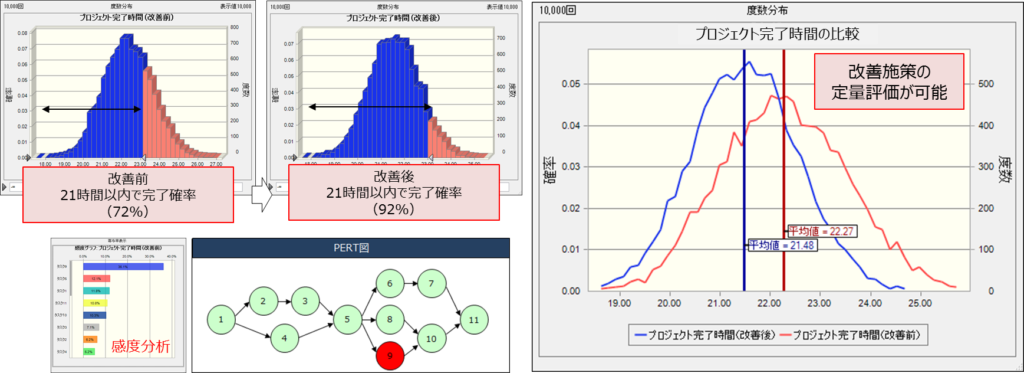
モンテカルロ・シミュレーションを実施しているためプロジェクト完了時間はヒストグラムとして見える化され、結果に対しての感度分析を行うことで結果に影響を与える要因を特定することができます。
本検討では、プロジェクト完了時間の平均値は22時間、ばらつき具合としての標準偏差は1.26時間、プロジェクト完了時間が23時間以内に収まる確率は72%となります。
不確実な要因に確率分布を定義しているためクリティカルパスも確率的に求めることが可能となりますが、本工程ではクリティカルパスの中で最も影響度の大きいタスクを洗い出し改善策を検討します。
感度分析によりタスク9が最も結果に影響を与える要因であるため何らかの改善策が必要であることがわかります。例えばタスク9の作業時間の変動幅を1~3時間にする施策を実施するとプロジェクト完了時間の平均値は21時間、 プロジェクト完了時間が23時間以内に収まる確率は92%となり20ポイント改善します。このように計画段階で重要な要因を特定するだけでなく、改善策の効果を定量的に説明することが可能です。
実務的にクリティカルパスを利用する場合はモンテカルロ・シミュレーションが適切
事業によっては工程計画の見誤りなどにより多額の損害を被ることもあります。 それぞれのタスクが影響しあって構成される工程にモンテカルロ・シミュレーションを適用することで、 リスクを考慮したクリティカルパス分析を行うことができ、計画の見直しや重要なタスクをあらかじめ把握することが可能となります。
Crystal Ball を利用すれば、Excelをベースとした簡単な操作でクリティカルパス分析が実施できます。無料期間もありますので、ぜひお手元で確認してみてください。