複利とリスク

シミュレーション

複利効果をExcelで再現したモデル

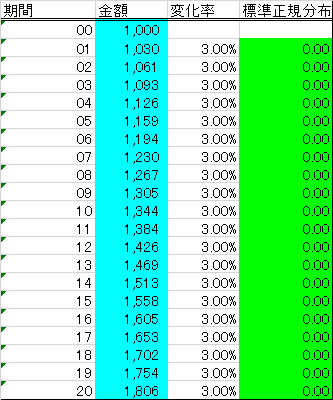
利用したシミュレーションモデルは、とても単純な形式としました。初期値は1,000で、20期間、毎期3.0%の利息が付くことにしています。 また、利息には15.0%のボラティリティを持たせることにしました。 利息と標準正規分布を組み合わせることで、毎期の変化率として表現します。

 シミュレーション結果

モンテカルロ・シミュレーションの実行と、複利による資産増加の傾向

特に深く考えず、100,000回のモンテカルロ・シミュレーションを実行してみました。 そのうち50回分を抽出して、グラフに表すと、下図の結果となりました。

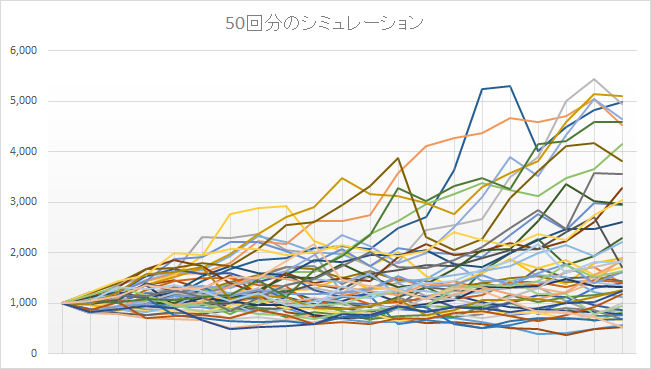
ざっと見た感じだと、初期値の1,000付近に集まっているシナリオが多いように見えます。 最終期間で最も大きな値となっているシナリオには、5,000を超えているものもあるようです。 逆に、最も悪いシナリオだと、500程度(初期値から半減)するものも発生しました。 100,000シナリオをすべて見るのは大変なので、結果の範囲をCrystal Ball の傾向グラフで表示すると 下記のグラフが得られます。赤い帯が中央値付近（45%～55%値）ですね。

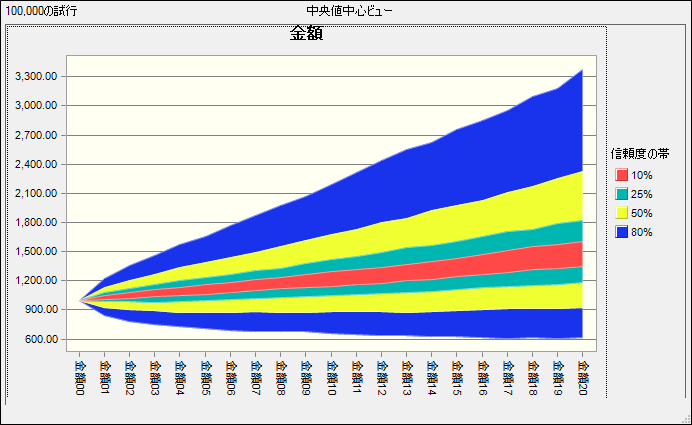
初期値が1,000で、毎期の利息が3%だとすると、複利で考えると20期後には 1,000×(1+0.03)^20 = 1,806 となってほしいのですが、1,800のラインは25%の帯の上端にあるため、複利の数値を超える可能性は 50%-(25%÷2) = 37.5% 程度であることがわかります。

シミュレーション結果を統計値で比較する

利息にボラティリティ（不確実性）がある場合の傾向として、時間が経つにつれて不確実性が大きくなること、 期待値（平均値）を上回る確率は、感覚的には50%であってほしいのですが、実はそれほどでもないことがわかりました。

傾向グラフの中でも、特に代表的な数値だけを抜き出してみたグラフが下図です。代表値として 10%値、中央値、期待値、90%値を表示し、さらに通常の複利計算と単利計算による 計算結果の線を載せてみました。

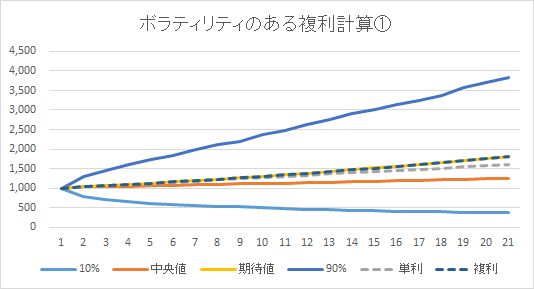
10%値と90%値の乖離が大きいため、これらの2値を取り除いて再度グラフを作成してみた結果が次の図です。

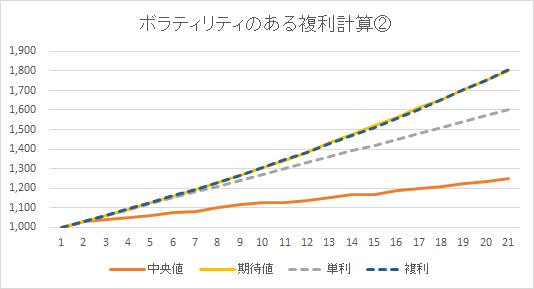
期待値と複利の値が一致することについては大体予想できていましたが、中央値が単利よりも小さくなっている点は意外でした。 期間を増やしたり、ボラティリティを変えてみたりすると、また別の結果を得られるのかもしれません。

Crystal Ball の予測グラフを活用してシミュレーション結果の詳細を確認

特定の期間に絞ってシミュレーション結果を確認してみます。今回は10, 20期間目の2箇所について、Crystal Ballの予測グラフを確認します。

グラフ内の「平均値」はこれまで書いている期待値のことです。 「信頼度」は、初期値1,000を上回る確率としました。まずは10期間目が以下です。

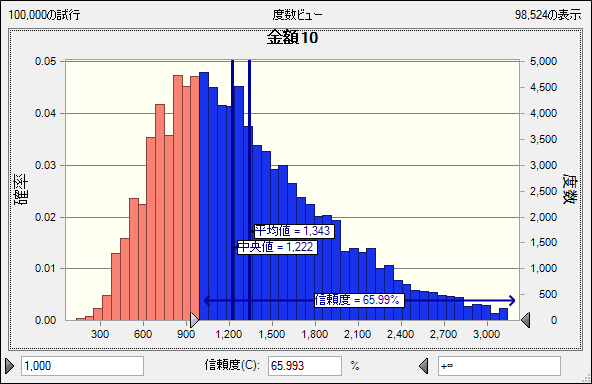
明らかに分布は左右対称ではないため、平均値、中央値、最頻区間に乖離が生まれていることがわかります。また、初期値を上回る信頼度は66%程度となりました。中央値を上回る確率が理論上はちょうど50%なので、平均値に到達する確率が50%を下回っていることも確認できます。

次に20期間目となります。

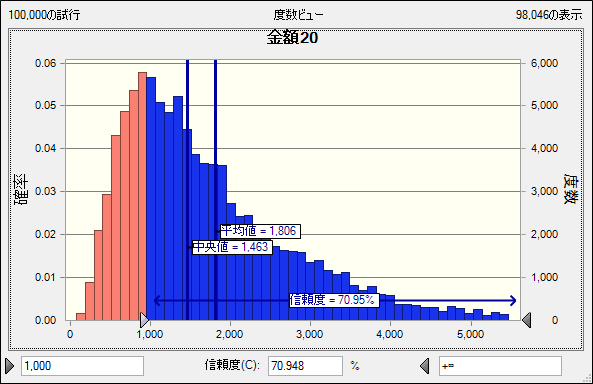
先の10期間目の結果と見比べると、分布の偏りが大きくなっていることがわかります。 一方で、初期値を上回る確率は71%程度と、先の結果よりも多少大きくなっています。

まとめ

一般的に良く知られている複利の計算にボラティリティ(ばらつき)を加えると どのような結果が得られるのかをシミュレーションによって確かめてみました。

ボラティリティを正規分布で表現したり、期間ごとのパラメータが変化しないなど、かなり簡易なシミュレーションモデルではありましたが、期待値以上の結果が得られる確率が普段思い浮かべる50%よりも小さくなってしまうという現象が確認できました。利用したExcelファイルは本ページ最上部で公開しておりますので、利息やボラティリティの数値を変えてみたり、 シミュレーションモデルを改造するなど、様々な分析を試していただければと思います。

構造計画研究所では、工学的な知見をもとにしたご支援を実施しております。今回のようなシミュレーションモデルの構築を含めて、興味のある方は是非お気軽にお問い合わせください。

お問い合わせフォームはこちら（リンク）

リスク分析のトップに戻る（リンク）

資料ダウンロード

弊社の個人情報に関する取り扱いについては「個人情報の取り扱いについて」（プライバシーマーク付与認定済）をご覧ください。