薬剤経済分析にモンテカルロ・シミュレーションを活用
薬剤経済分析は効用などの経済学の考え方を元にして、費用対効果を考える手法となります。本記事ではシミュレーションの前に、薬剤経済分析がどのような考え方をとるのか確認します。
薬剤経済分析とモンテカルロ・シミュレーションの導入
※本記事はモンテカルロ・シミュレーションを実施しません。次の記事(準備中)にて実施していきます。
医薬品への選好?
突然ですが、皆様はどのような視点で薬を選びますでしょうか。最近では、従来薬(先発品)と効果に差がなく価格が安価なジェネリック(後発品)を目にする機会も増えてきました。ここでポイントになるのは「どちらの医薬品のほうが良いのか」という視点です。
消費者目線ではあまり考えないかもしれませんが、実際に「どちらの医薬品のほうが良いのか」という観点は、国・政府機関においても重要です。なぜならその価値の評価が薬価の設定などにつながり、さらには医療費にもつながってくるためです。欧米諸国ではこのような薬剤経済評価のためのガイドラインが公表されており、定量的な分析・評価が行われています。そこで今回は、英国の国立医療技術評価機関“NICE”などで採用されているICERをご紹介します。 (次号以降では、Crystal Ballとの融合を考えてみます)
質調整生存年の考え方
ここではまず「質調整生存年」という言葉をご紹介します。
質調整生存年は1つの単位「QALY(s)」で数え、1QALYは「完全な健康状態で過ごす1年」を表します。反対に、死亡してしまった場合は0QALYです。何をもって「完全な健康状態」とするか、数値化には様々な手法があり、今回その部分は省略しますが、新しい薬や医療機器が世に出てきたときには「どれくらいQALYが伸びるか」が焦点になります。
薬の種類と効用値
例えば以下の例を考えてみます。
とある疾患に対して薬Aを使用すると、だんだんと効き目が弱くなり10年後に死亡してしまうとします。一方で薬Bを使うと、10年後に死亡してしまうのは変わらないものの、その間の通院頻度や入院期間を減らすことができるとします。
さらに、患者に対する生活の健康状態に対する満足度を0.0~1.0で表現した効用値を用いて、 薬A、Bそれぞれの効用値の変化を以下のようにプロットしたとします。
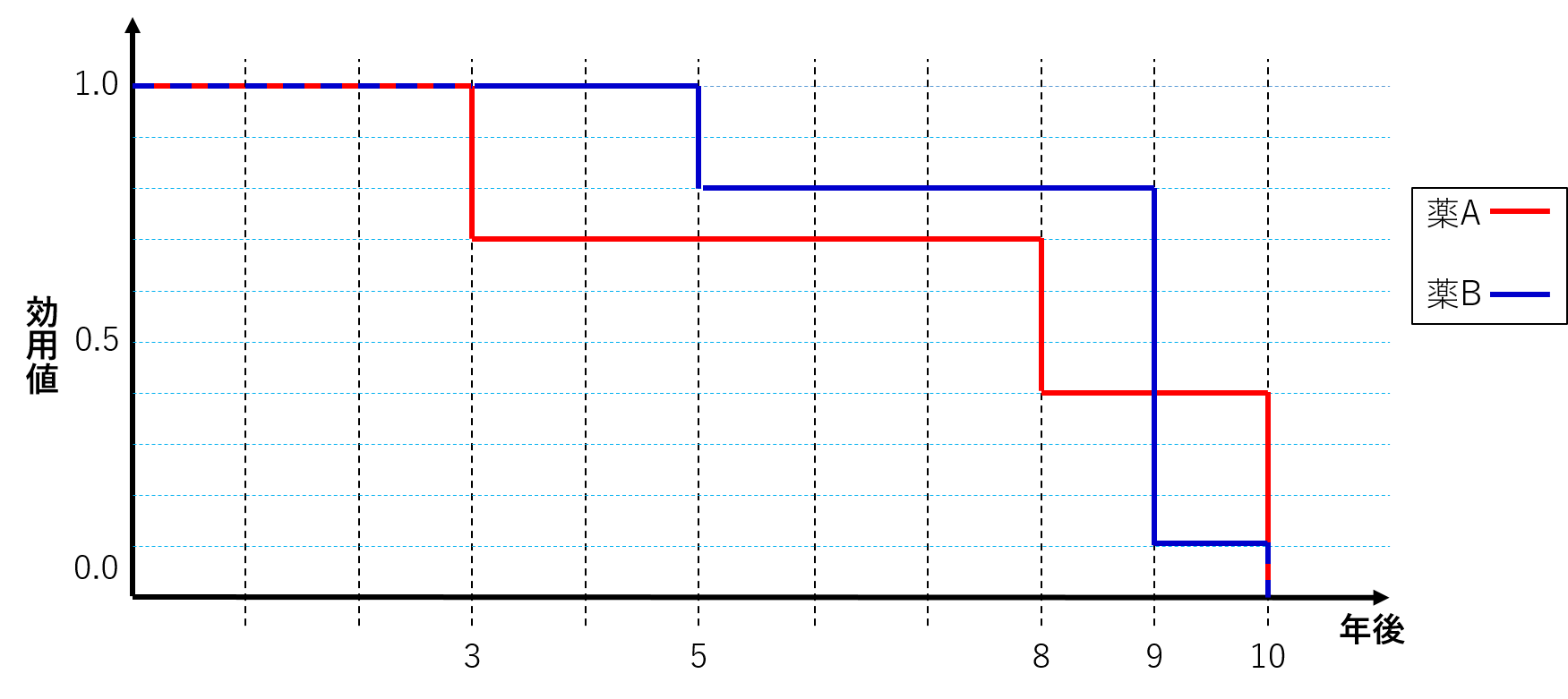
この時のQALYはそれぞれ、以下のように計算されます。
- QALY(薬A)=1.0×3+0.7×5+0.4×2=7.3[QALY]
- QALY(薬B)=1.0×5+0.8×4+0.1×1=8.3[QALY]
つまり、薬Bを服用した人のほうが、1年長く完全な健康状態を過ごすことができた、ということになります。
QALYとコスト
この2つの薬A、B対してコストの概念を埋め込んでみます。薬Aを用いる治療法のコストが1000万円、薬Bを用いる治療法のコストが1700万円であるとします。このとき、薬A、Bの費用対効果は、それぞれ以下のように算出できます。
- 薬A:1000÷7.3=136.99[万円/QALY]
- 薬B:1700÷8.3=204.82[万円/QALY]
この場合、薬Aのほうが値が小さいため費用対効果は薬Aのほうが良いということになります。
一方で、薬BのほうがQALYが大きいことから、薬Bに切り替えるメリットもありそうです。この場合は、以下の数式によって増分を検証します。
- (1700-1000)÷(8.3-7.3)=700[万円/QALY]
この分析方法を増分分析と呼び、700[万円/QALY]を増分費用効果比と呼びます。英語にするとIncremental Cost-effectiveness ratioとなることから、頭文字を取りICERとも言われます。
先ほどの例では「薬Bに切り替えた場合は1QALYを得るために700万円追加が必要」という意味になります。問題はこの700万円が高いかどうかという話になりますが、概ね 、米国:5~10[万ドル/QALY]、英国:2~3[万ポンド/QALY] 以下であれば、費用効果的であるといわれています。日本円に換算すると500~1000[万円/QALY]です。 そう考えると、薬Bはまさにボーダーラインといえます。
まとめ
今回は簡単な費用対効果分析についてお話いたしましたが、本来であれば薬を服用したときの様々なイベントや発生確率を考慮して分析をする必要があります。次号以降では、分析の幅を広げてCrystal Ballとの融合を考えてみます。
参考文献
京都廣川書店 発行(2011年) 恩田 光子、砂川 雅之、森脇 健介、栁澤 振一郎 著 「詳説 薬剤経済学」
資料ダウンロード

弊社の個人情報に関する取り扱いについては「個人情報の取り扱いについて」(プライバシーマーク付与認定済)をご覧ください。
