モンテカルロ・シミュレーションによるストックオプションの評価(基礎編)
株価をExcel上でランダムウォークさせた上で、ストックオプションの諸条件を元にして価値を算定していきます
ストックオプションの公正価値評価
複雑化する条件のためシミュレーションが必要となる
ここ数か月の間に、ストックオプションという報酬制度の評価額を算出するために モンテカルロ・シミュレーションを行う方法を知りたいというお問い合わせが増えています。
色々と資料を探して見ていると、この制度を評価するためには、ブラック・ショールズモデルなどの金融工学的な方法をとる場合が多いようです。 ただし、制度に細かな条件(オプション)を加えていくと、必ずしも方程式で答えが出せるような 形式にならない場合があるということで、確率的な評価を行うことができるモンテカルロ・シミュレーションの出番が出てくる、というわけです。
細かいことを書いていくとキリがなさそうなので、本記事では「オプション価格の評価式を使って 理論値とシミュレーション結果がどれくらい違うのか」という点と、「確率的な理論がある場合の シミュレーションモデル作成」について、ご紹介いたします。
ストックオプションについて
制度上のストックオプション
ストックオプション制度というのは以下のような制度のことです。
会社役員や従業員等があらかじめ定めた価格で自社株式を購入できる権利をいいます。株価が行使価格を上回れば、その差額がそのまま報酬となるため、ストックオプション制度は、会社役員等に対する業績連動型のインセンティブ報酬として、利用されています。
日本取引所グループ用語集「ストックオプション」
ストックオプション制度を利用する人は、以下の手順で報酬を得るということのようです。
- 会社の株式を、ある金額で買う権利を得る。
- 期日に株価が上がっていれば、権利を行使して報酬を得る
- 期日に株価が下がっていれば、権利を放棄する
会社の業績向上は株価上昇に繋がると考えられるため、権利を与えられた人にとっては 業績を上げることがインセンティブになり、会社と従業員、はては株主にとっても嬉しい制度というところでしょうか。
オプション価格の評価について
また色々と調べていくと、ストックオプションによる報酬は費用計上が必要らしく、 会社側としてはこのストックオプションの評価額を算定することになります。
ストックオプションは、金融工学における「コールオプション」に分類されるため、評価額の算定の基礎として ブラック・ショールズ式などが活用されます。たとえばコールオプション(ヨーロピアン・コールオプション)の価値は ブラック・ショールズ式で理論的に計算することができます。
数式の中のSが株価、μはドリフト係数、rは無リスク金利、 σはボラティリティ、Cがコールオプションの価値、kが権利行使価格です。 また、dWは確率過程(ウィナー過程)、N()が正規分布の累積分布、eがネイピア数を表しています。

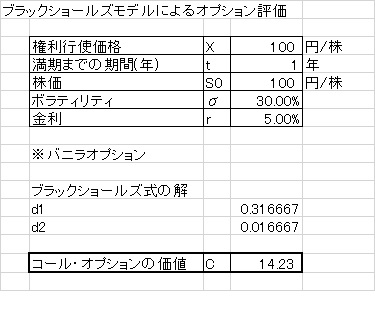
理論上正しい計算式があれば、各パラメータを入力することでExcelでも簡単に答えを得ることができます。また、Excelで正規分布の累積分布関数を計算するには、NORM.S.DIST関数を使うことになります。本ページ下部にサンプルファイルのお申し込みがございますので、ぜひご活用ください。
モンテカルロシミュレーションを使った算定方法
Crystal Ball で算出
理論解(解析解、厳密解とも呼びます)がある場合は計算式が決まっているので良いのですが、上記のコールオプションに加えてノックアウト条件などの追加オプションを加えるような場合には 理論解を計算するのは大変なので(できるかどうかわからない)、シミュレーションを使って近似解を求める方法が役に立つことがあります。
近似解は名前の通り「答えに近い値」なので、応用的な算定を行う前に 理論解が分かっている問題で、どれくらい答えが違うのかを確認しておく必要があります。
また、シミュレーションを利用した方法では、解を得るために計算対象の動きをモデル化する必要があるため、問題の本質を理解することにも役立ちます。 今回の例では、以下のステップでモンテカルロ・シミュレーションを行い、オプション価値を算定してみました。
- 株価の変動モデルを作成する
- 満期時の株価と権利行使価格の差(ペイオフ)を計算する
- ペイオフの期待値を現在価値に割戻して、オプション価値を算定する

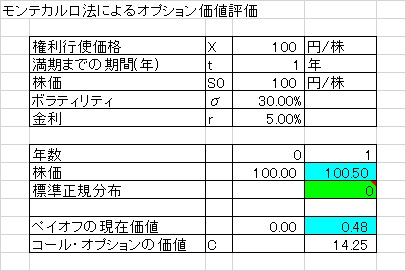
ExcelとCrystal Ballを用いると、以下のような表現が可能です。 使用している仮定は標準正規分布です。また、ペイオフの期待値を取得するために、 Crystal Ballのワークシート関数「CB.GetForeStatFN(ペイオフ,2)」を使用しました。 最初の状態はエラーですが、Crystal Ballのシミュレーションを実行することで値が入ります。
なお、今回利用したExcelファイルは本ページ下部にて無料でお配りしております。Crystal Ball の15日間無料体験と合わせて、ぜひご利用ください。
10,000回のモンテカルロ・シミュレーションを実行して計算結果を比較すると、概ね近い値になりました。理屈の上では、モンテカルロ・シミュレーションの試行回数を増やすとより理論解に近づいていきます。
- ブラック・ショールズ式の答え:14.23
- シミュレーションで得られた答え:14.25
また、Crystal Ballの予測結果を確認すれば、具体的にどの部分がオプション評価値となっているのかなどの情報を視覚的にも得ることができるため、問題への理解も深まります。
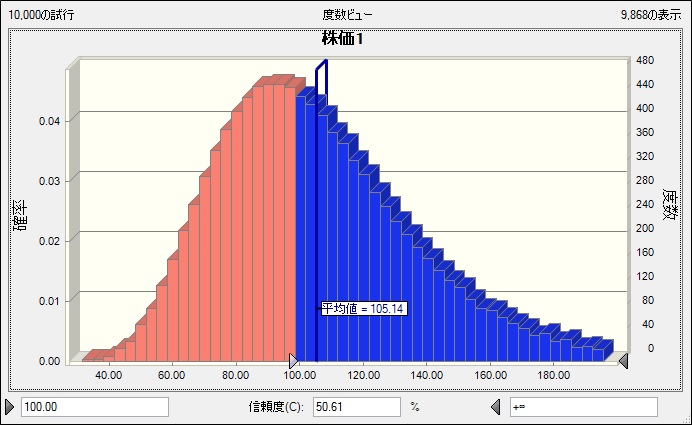
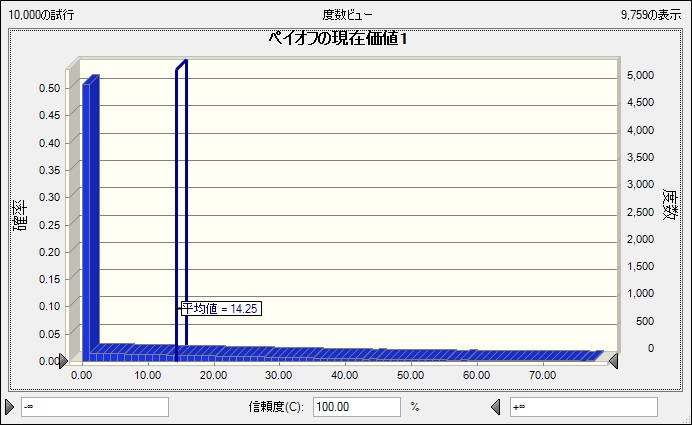
シミュレーションモデルを使用する場合は、対象(今回は株価)の変動からモデル化するため、 対象の動きに合わせて何かアクションを起こす計算式を加えていけば、複雑なオプションの評価モデルを作成することも可能になります。この際に気をつけなければいけないこともあるのですが、また別の機会にご紹介したいと思います。
活用してみましょう!
Crystal Ball を活用してモンテカルロ・シミュレーションにより簡易にストックオプションの公正価値算定を行いました。今後、複雑化していくであろう条件付けにもExcelワーク次第で対応していくことが可能です。
今回利用したサンプルファイルは無料でお配りしております。また、シミュレーションを実行するために必要となるCrystal Ball も15日間の無料体験期間がございます。サンプルファイルとCrystal Ball (無料体験)は、いずれも以下のリンクからダウンロード可能です。今回指定した株価やボラティリティなどの数値を変更してシミュレーションしてみることが可能です。ぜひお手元でお試しください。
また、詳細の説明やデモに興味がある、こんなケースでも利用できるか確認したい、という場合には、ぜひ担当者までお問い合わせ(リンク)ください
サンプルファイルのダウンロード
弊社の個人情報に関する取り扱いについては「個人情報の取り扱いについて」(プライバシーマーク付与認定済)をご覧ください。
