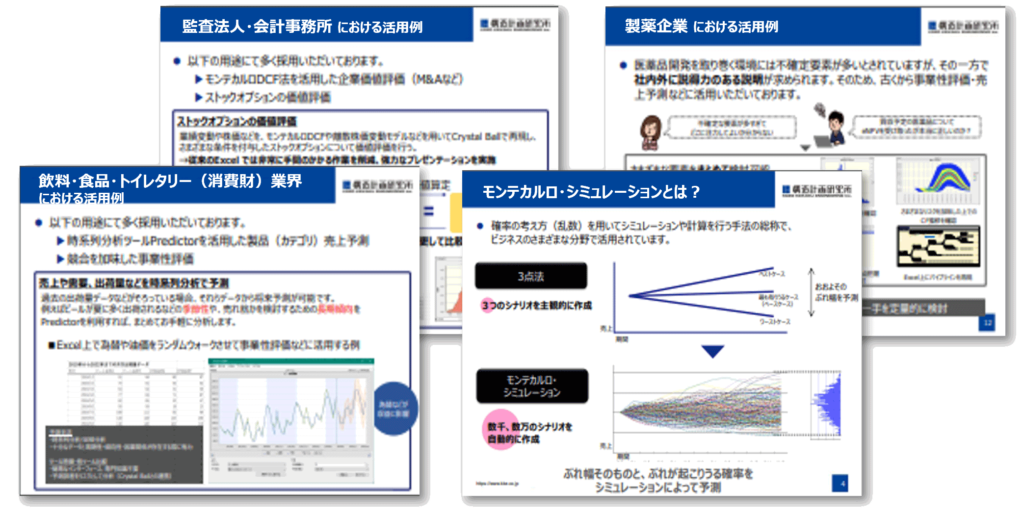
Crystal Ballを用いた設備の故障率と修復時間の確率的な分析
設備・システム・プロセスなど、故障率や修復時間などが検討される領域においては、確率的な分析が盛んに実施されます。ここではCrystal Ball を用いた設備故障の分析例を取り上げます。
設備の故障率と修復時間の重要性
全体の停止時間を最小化するため
設備の効率的な運用には、故障率と修復時間の管理が不可欠です。これらの要素を適切に分析することで、全体の停止時間を最小化し、生産性を向上させることができます。Crystal Ballを使用して、これらの要素を確率分布としてモデル化し、シミュレーションを行います。感度分析により、改善すべき要因を明確にします。
こうした確率的な分析は、ありとあらゆる設備・システム・プロセスに適用可能です。例えば、以下のようなケースが挙げられます。
- 発電所におけるメンテナンスと機会損失の分析
- システムへの投資や可用性に関する分析
- 銀行など窓口業務の最適化
本記事では分析例として、工場内に複数ある設備が故障した場合の総停止時間をCrystal Ball を活用して分析します。
Crystal Ball を活用した停止時間の確率的な分析
分析の前提
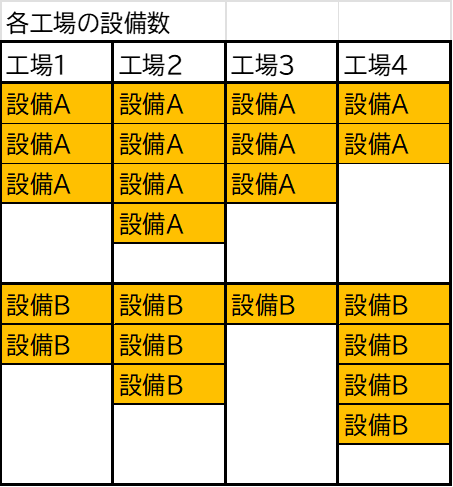
設備がAとBの2種類あり、AとBでは故障率と修復時間が異なります。これらの積として停止時間を求めます。なお、設備が導入されている工場は4か所あり、それぞれの工場で設備の導入台数が異なると仮定します。
ポアソン分布による故障率の設定
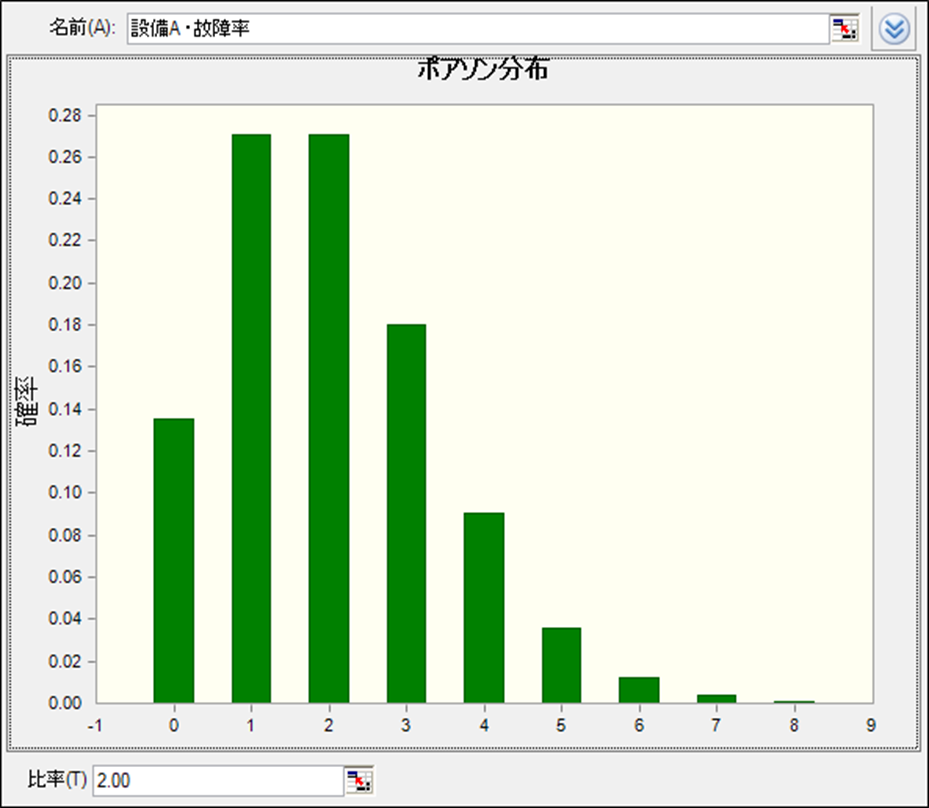
ポアソン分布は、一定の時間内に発生するイベント(この場合は設備の故障)の回数をモデル化するのに適しています。故障率λを設定し、月当たりの故障回数を予測します。例えば、λ=2の場合、月平均2回の故障が発生することを意味します。
以下のように設備Aでは月平均2回、設備Bでは月平均2.4回の故障が起きる仮定を置きます。
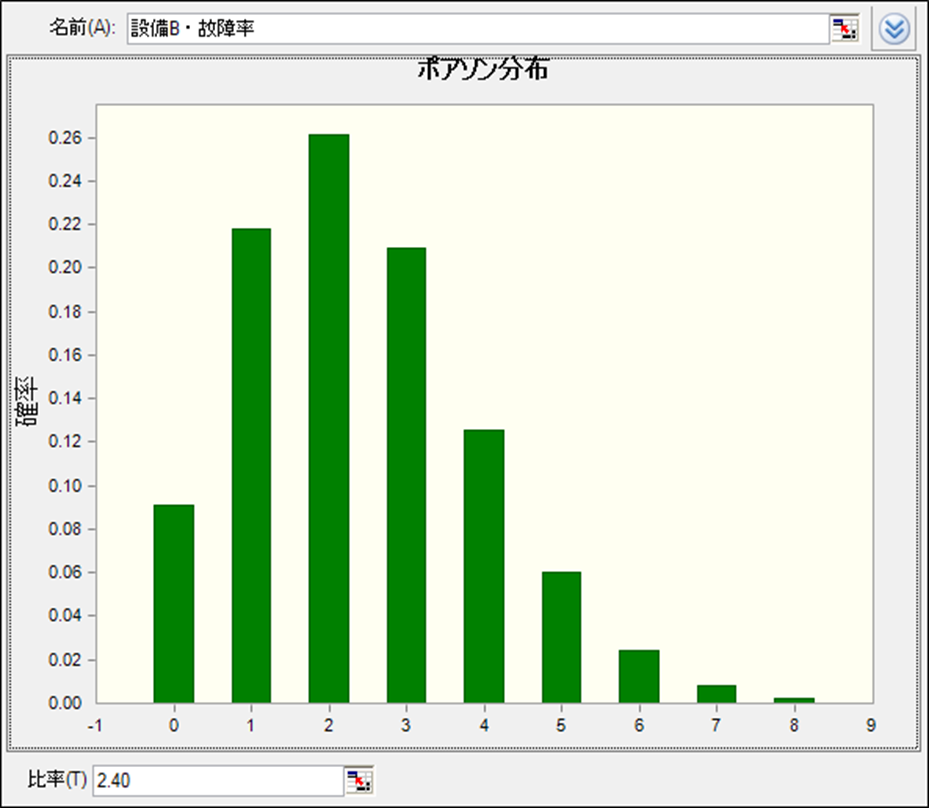
故障頻度を表すとされるものにバスタブ曲線というものがあります。設備の導入時期を切り口とした場合の故障発生の頻度や改善目標を示すものとなり、ポアソン分布と異なります。別の記事で触れたいと思います。
修復時間の確率分布設定
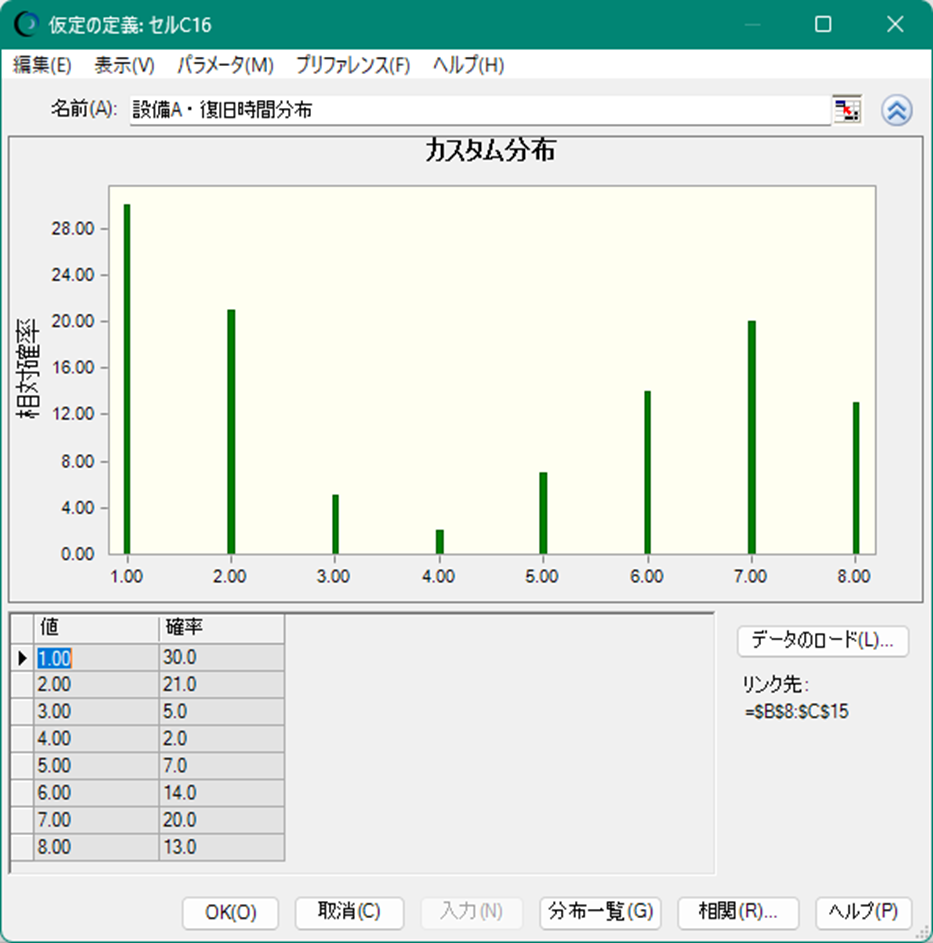
修復時間も確率分布を用いてモデル化します。ここでは、過去の修復時間データが入手できたと仮定して、そのデータをそのまま確率分布として利用していきます。Crystal Ball のカスタム分布という機能を利用しています。
他の設定方法には、修復時間が平均やばらつきがある場合、正規分布などを使用してモデル化できます。

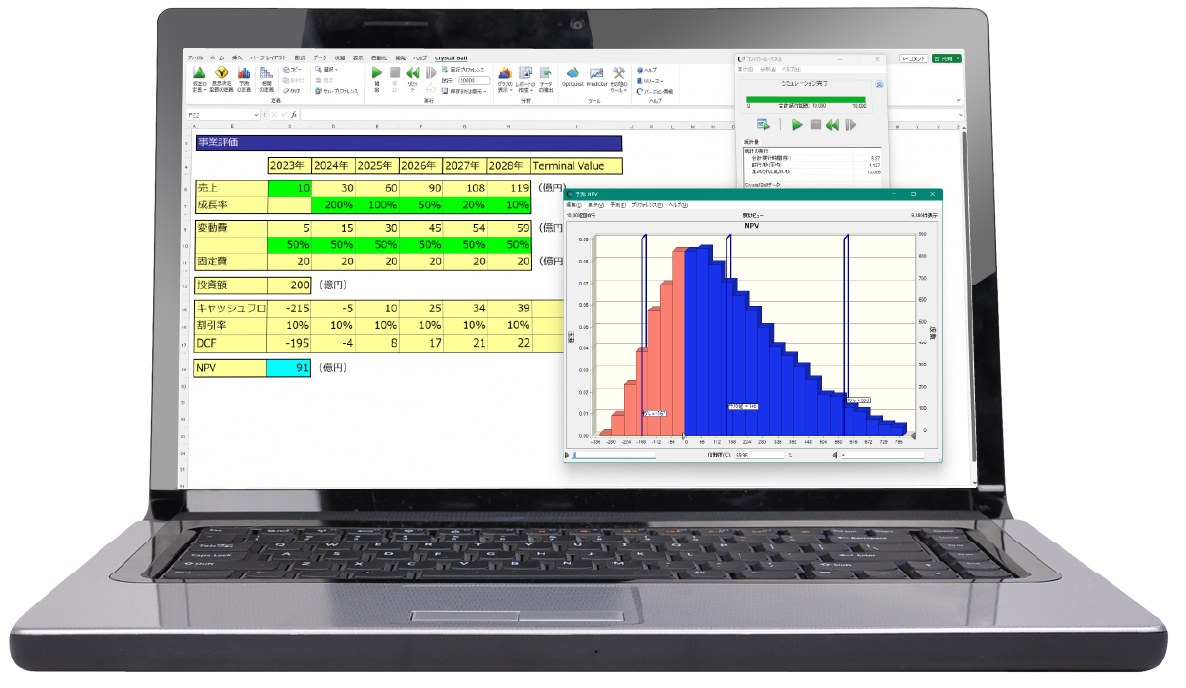
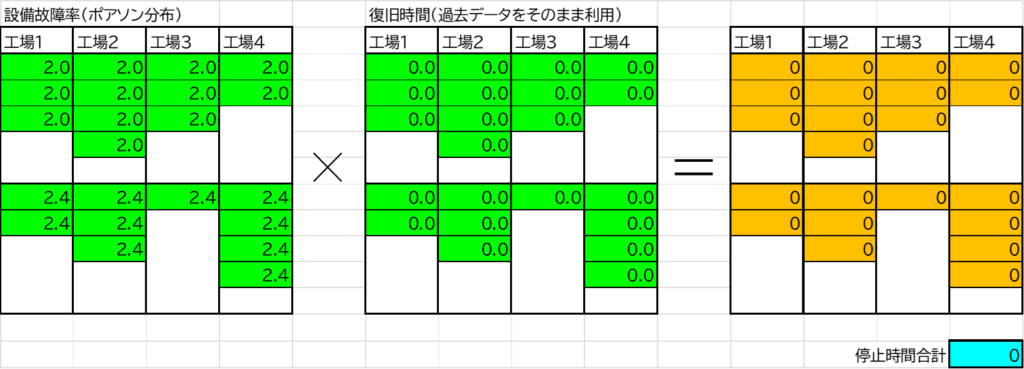
全体の停止時間の計算
故障率と修復時間の確率分布を掛け合わせることで、全体の停止時間を計算します。これにより、年間の総停止時間をばらつきをもって予測します。例えば、停止時間を200時間以内に抑えられる可能性が20%しかない、といった分析が可能となります。
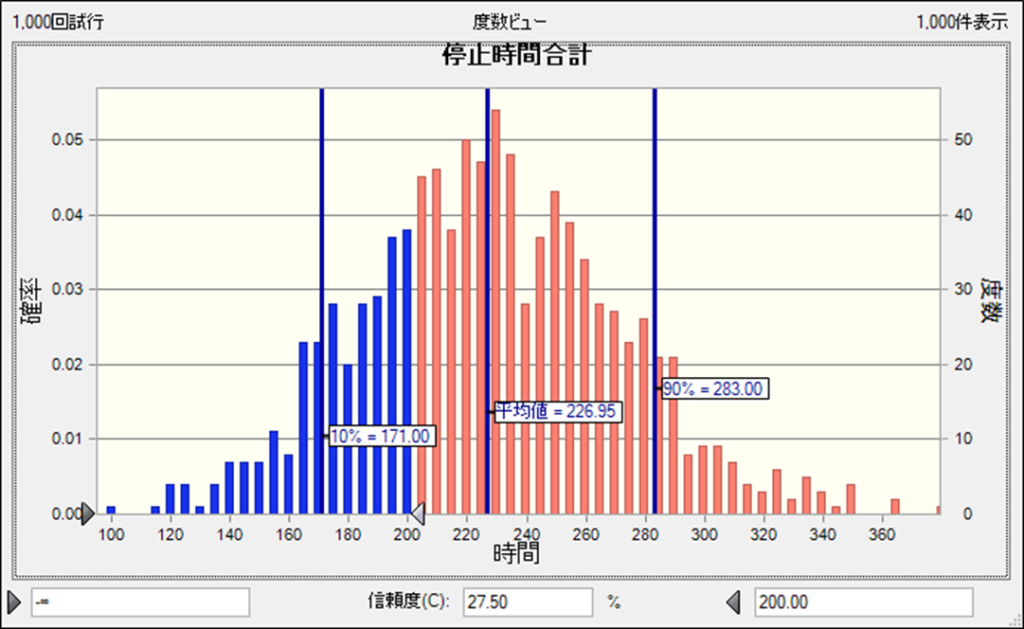
分析結果は以下のようになりました。停止時間の平均値は226時間、10%値は171時間、90%値は283時間、また、停止時間が200時間に収まる可能性は27.5%と計算されています。
感度分析による改善点の特定
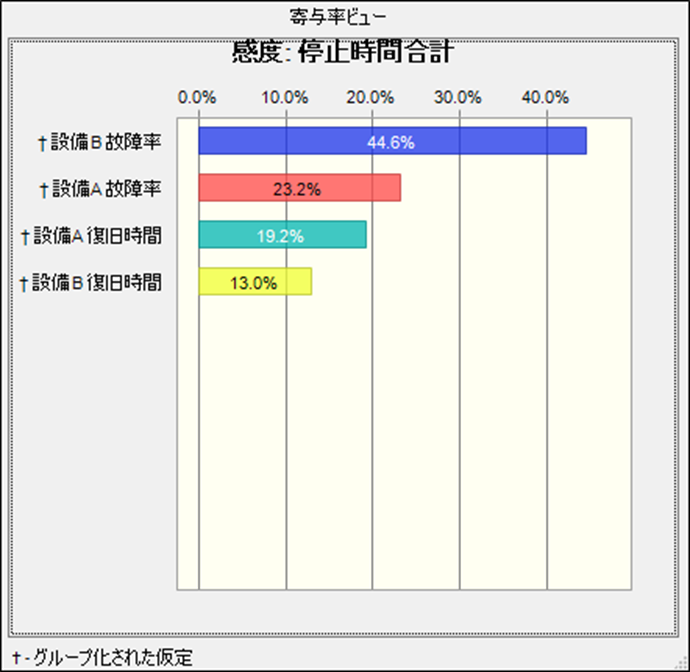
感度分析を行うことで、全体の停止時間に対する故障率と修復時間の影響度を評価します。ここでは実施しておりませんが、工場別での分析も有用かもしれません。どの要因を優先的に改善すべきかを明確にします。
分析結果として、設備AとBのいずれも故障率を改善した方がよいようです。特にBの影響が強いようです。
確率的な分析はCrystal Ball で手軽に実施
設備の故障率と修復時間を確率をもって分析し、全体の停止時間を予測しました。感度分析を通じて、どの要因を改善すべきかを明確にすることで、生産性を向上させ、効率的な設備運用を実現します。これにより、効果的なリスク管理と最適化が可能となります。
ここで利用したCrystal Ball は Excelベースで確率的な分析ができる優れたツールとなっております。他にも、トルネード分析、相関分析、ブートストラップ法、時系列分析、数理最適化ツールなど、便利な機能が付属するツールとなっております。
本例では生産管理の担当者や、QC活動を行われている方、生産工程改善を試みるエンジニアリングコンサルタントなどを想定して記事を書いておりますが、冒頭にも挙げたように工場に限らず、さまざまな設備・システム・プロセスなどで実際に利用されています。
本ページ下部に業界別の利用についてまとめた資料を記載しております。ビジネスにおける確率的な分析の事例について、ぜひお手元でご覧ください。