モンテカルロ・シミュレーションでは「乱数」が重要

そもそも乱数とは？

本記事ではモンテカルロ・シミュレーションや、乱数を活用する際に重要な検討項目となる、サンプリング手法について扱います。この説明をする前に、まずは乱数について抑えていきましょう。そもそも乱数とは何でしょうか。

英語で説明を誤魔化してしまえば、ランダムな数となります。手元に「乱数の知識」という1970年に出版された書籍がありますが、これによれば「等確率性」と「無規則性」を満たすような数列（たくさんの数）を指すようです。これについてはさまざまな定義があります。

乱数は何かを決める際に、とても好まれます。2人でどこに行くか決めたいが迷っているシチュエーションを想像してください。1人はファミレスでサンドイッチを食べたい、もう1人は中華料理屋で天津飯を食べたかったとしましょう。そこで、サイコロで1,2,3が出たらファミレスに、4,5,6が出たら中華料理に行くことにしてサイコロを振ってみます。サイコロの持ち合わせはないかもしれないので、スマホのアプリや（ルーレットもあります）、財布にある小銭の裏表でも代用できるかと思います。

なぜ2人はサイコロに意思決定を任せられたのでしょうか。それは2人の意思を離れて公平だからです。サイコロは、恐らくファミレスにも中華にも興味がないでしょう。どちらかに肩入れしていれば、2人のどちらかは納得がいかなかったはずです。その意味で乱数は、とても頼れる第3者とも言えます。

PCのスペックと乱数の生成

そんな乱数ですが、ビジネスでも活用されています。大きな活用先としてモンテカルロ・シミュレーションが挙げられます。こちらについては別のページでご紹介しておりますので、ぜひご覧ください。

乱数を作ると一口に言っても、かなり厄介ではあります。例えばExcelにはrand関数というものが用意されておりますが、あまりに多くのrand関数を、他の多くのExcel式と共に置いておくと、Excelシートの動作はかなり重くなります。このように、乱数の取り扱いはPCのスペックとの闘いになりがちです。現に、乱数の生成スピード（どのぐらいの速さで乱数を作れるか）や、その精度（ちゃんとランダムになっているか、偏りがないか）について、多くの技術者・数学者が闘いの歴史を繰り広げてきました。

そのような経緯から、乱数の作成方法についての検討は長い年月をかけて深まっていきました。これが本記事で取り扱う「サンプリング」という技術になります。おかげさまで、乱数を用いたビジネスリスク分析を簡単に実施してくれる Crystal Ball では、「サンプリング手法」を選択できるようになっています。

Crystal Ball で扱うことができるサンプリング手法

サンプリング手法とは何か

全国チェーンのスーパーマーケットで、10日間に1万個売れたチーズケーキという宣伝がされていました。翌月のチーズケーキの仕入れ量を決めるため、販売数に関するシミュレーションを実施してみましょう。

ある店舗では、1か月間に約300個のチーズケーキが売れるとします。幅としては、200個～500個の販売数であることも分かっています。この時、チーズケーキの販売数を確率分布で表してみると以下のようになります。ここでは三角分布を利用しました。

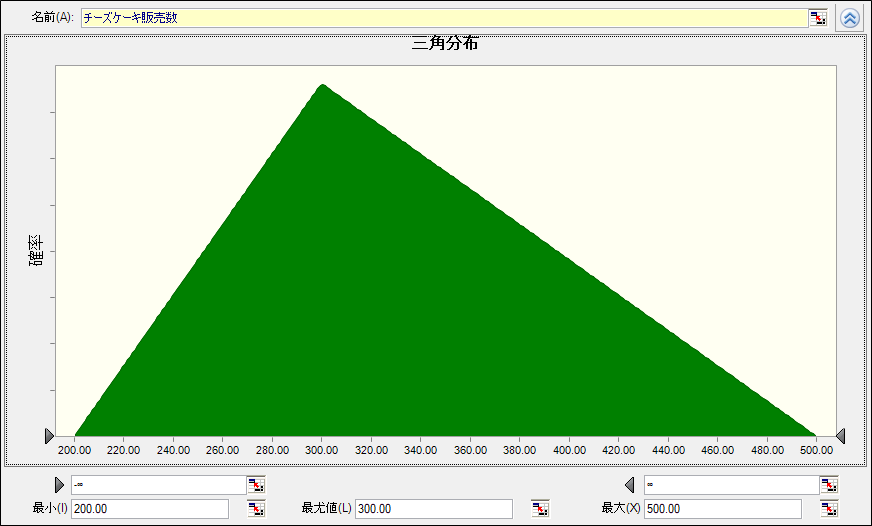
ここで、仮に、試行回数を3回としてシミュレーションを実行してみたとします。そのとき、301個、326個、340個の3ケースが発生したとしましょう。これがサンプリングとなります。つまり、確率分布などの仮定に基づいて乱数を作成するプロセスの事となります。

では実際に、試行回数を10,000回としてCrystal Ball でシミュレーションを実施してみましょう。すると、以下のようになりました。少し見にくいですが、背景の緑色の三角形が元々設定した確率分布となります。その確率分布に基づいて作成したランダムな10,000ケースが手前の青色のヒストグラムとなります。青色はかなりギザギザになっており、緑色から外れている箇所が散見されるかと思います。

• 表示方法：シミュレーション実行後、[グラフの表示] > [仮定グラフ] より、当該の仮定セルを選択

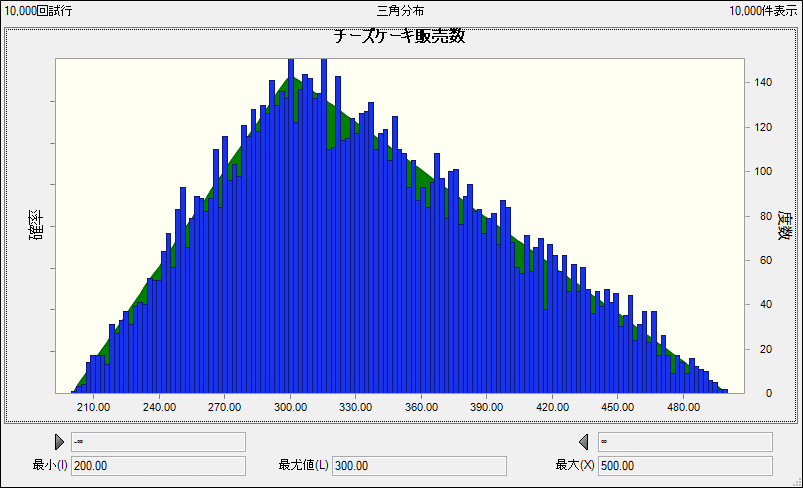
青色と緑色が一致していない箇所、ギザギザの箇所は、乱数の発生に偏りがあったことを示しています。本来であれば、320個も330個もおよそ同じぐらいの確率で起こるべきところを320個はあまり起こらず、330個は多く起こっていたといった具合になります。

サンプリング手法による結果の違い

次に、Crystal Ball に搭載されている別のサンプリング手法を試してみて、結果の違いを比較してみましょう。

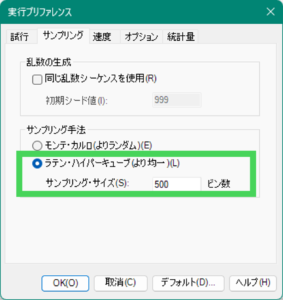
まずは、以下の画面にて、サンプリング手法を選択します。今回は「ラテン・ハイパーキューブ」を選択してみましょう。なお、上記のシミュレーションでは「モンテカルロ」が選択されていました。Crystal Ball をインストールした際には、最初はモンテカルロ法が設定されています。

• 設定方法：実行プリファレンス＞サンプリング＞サンプリング手法＞ラテン・ハイパーキューブにチェック

ラテン・ハイパーキューブを選択後に、上記と同じシミュレーションを実施して、先ほどと結果を比較したものが以下となります。モンテカルロに比較して、ラテン・ハイパーキューブの方が「ギザギザ」が小さく、想定した確率分布に近い乱数が作成されていることがお分かりいただけるかと思います。

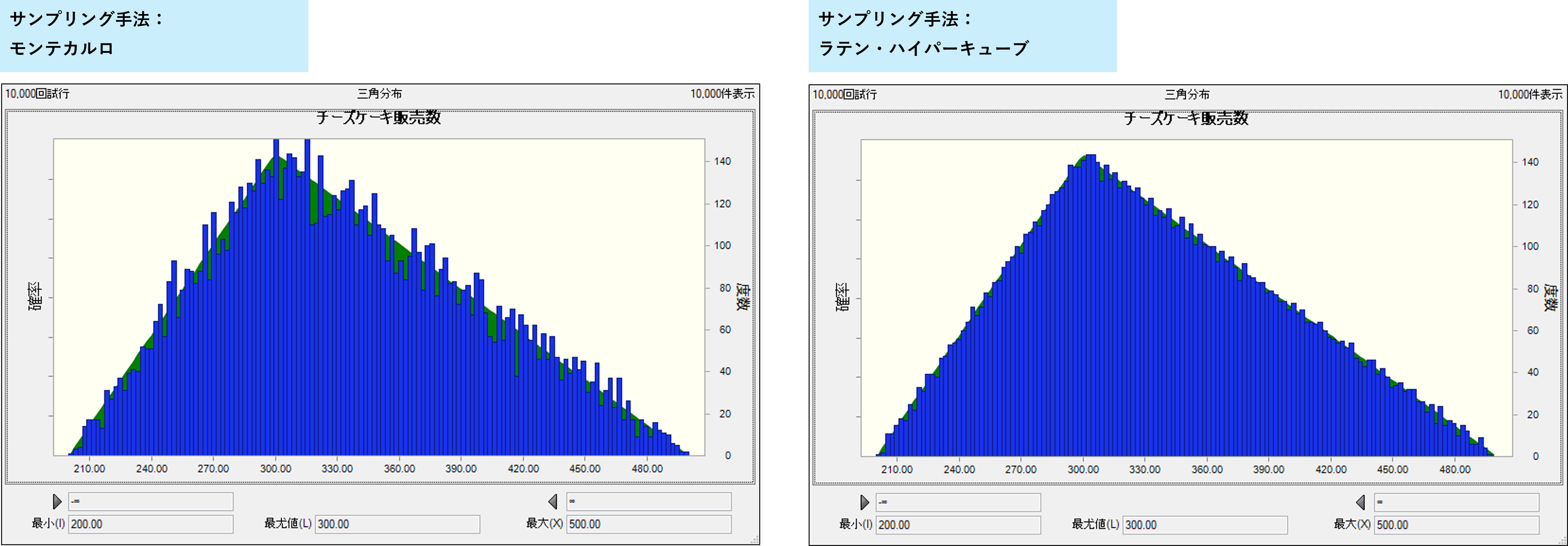
ラテン・ハイパーキューブという手法では、範囲ごとに乱数を作成しています。イメージとしては、200個～210個に収まるように1試行、211個～220個に収まるように1試行、... といった風に、設定した確率分布と矛盾しないように調整しつつ、シミュレーションを実施しています。さらに言えば、「400個以上の販売数になることは1回も起きない」というケースを減らすことができます。より想定に近い、均一な結果を得ることが可能となります。これがラテン・ハイパーキューブの特徴となります。

モンテカルロを選択した場合には、上記のような調整は一切行われません。偏ったケースも（人間の感覚ですが）多く発生します。

メリット・デメリットについては次の章に譲りますが、まずはこれがサンプリング手法による違いとなります。それではすべてのケースにおいて、ラテン・ハイパーキューブを活用して、きれいな結果を得られればよいのでしょうか？

サンプリング手法ごとの使いどころ

主たるサンプリング手法の違いのまとめ

Crystal Ball では「モンテカルロ」と「ラテン・ハイパーキューブ」という2つのサンプリング手法が利用できます。それぞれ、モンテカルロ・サンプリング（Monte Carlo Sampling : MCS）、ラテン・ハイパーキューブ・サンプリング（Latin Hypercube Sampling : LHS）と呼ばれることもあります。

上記の比較を通じて、ラテン・ハイパーキューブはモンテカルロと比べて、きれいな結果が得られることが分かりました。違いをまとめると以下のようになります。

サンプリング手法	メリット	デメリット
モンテカルロ	ランダムさを重視できる	（ラテン・ハイパーキューブと比較して）結果に偏りがある
ラテン・ハイパーキューブ	（モンテカルロと比較して）少ない試行回数で理論値に近い値を得られる	メモリが多く必要になり、シミュレーション実行時間が延びる

では、どちらを使えばいいのでしょうか。

ラテン・ハイパーキューブのメリットしては効率性となります。つまり、「少ない試行回数」でモンテカルロの選択時と同じ水準の結果が得られるというメリットがあります。特に、平均やパーセンタイル値などの統計量は理論値に近い値を容易に得られます。しかし、その手法の特性上、偏りが出にくいという特徴がありますので、偏ったケースを特に確認したい場合には注意が必要です。

先ほどモンテカルロではより偏ったケースが発生すると述べました。モンテカルロ・シミュレーションの目的によっては、その偏ったケースに注目したい場合もあります。シミュレーションはよく、単なる起こり得そうな将来を把握するためではなく、通常であれば起きえないようなケースの発見を目的とすることがあります。例えば、保険業界におけるモンテカルロ・シミュレーションの使われ方です。

保険会社は各取引先への保険支払金を準備しておく必要がありますが、通常では起きえない規模の災害などにより、保険金支払いが同じタイミングで発生してしまい支払いが滞るというケースが存在します。そのような場合を防ぐために、保険会社は事前に支払金を計算して、それが大きくなりすぎないように契約数をコントロールしたり、支払い能力を超える契約については再保険に回すなどの対応が取られます。

そのような場合には、通常起きないような「稀」なケースを想定しておく必要があります。とはいえ、ラテン・ハイパーキューブではなくモンテカルロの選択をお勧めするわけではありません。Excelシート、シミュレーションのモデルに依存します。また、そのようなケースでも偏りではなく理論値こそが重要という声もあるかと思います。いずれにせよ、違いを意識しておくことで、より意図に沿った、効率的な、シミュレーションが実施できるかと思います。

サンプリング手法の違いについて、お手元のExcelシートでお試しください

本記事ではサンプリング手法の違いと選択方法について記載いたしました。Crystal Ball を活用すると、その違いを簡単に試すことができます。インストールいただければ、15日間は無料で試用できますので、ぜひお試しください。

試用版のご案内

15日間、全ての機能を体験できます。 製品版と同じ Crystal Ball にはスタンダードパックとプロパックがございます。プロパックはスタンダードパックの全ての機能に加えて…

Crystal Ball - モンテカルロ・シミュレーションによる意思決定支援ソフトウェア

また、弊社は技術コンサルティング企業として、様々な分野における統計やシミュレーションを扱い、ご支援をさせていただいております。お困りの際にはぜひお声がけください。

（本記事は内容に関しまして正確を保つように努めておりますが、その正確性、完全性、最新性等を保証するものではございませんのでご了承ください）

資料ダウンロード

弊社の個人情報に関する取り扱いについては「個人情報の取り扱いについて」（プライバシーマーク付与認定済）をご覧ください。