モンテカルロ・シミュレーションによるストックオプションの評価(応用編)
応用編では特にノックアウト条項を扱います
ストックオプションの公正価値評価
複雑化する条件のためシミュレーションが必要となる
基礎編では、ストックオプションの公正価値評価にモンテカルロ・シミュレーションを活用するというフレームをお伝えしました。ぜひご覧ください。
→基礎編:モンテカルロ・シミュレーションを活用したストックオプションの公正価値評価(リンク)
今回は、このストックオプションに、以下の条件を加えてみたいと思います。ノックアウトの判定を行うために、シミュレーションのモデル構築においては「離散化」というテクニックを使います。
期間中に株式が一定価格を下回った場合は、権利を失う。(ノックアウト・オプション)
オプション価格の評価
ストックオプションは、金融工学における「コールオプション」に分類されるため、評価額の算定の基礎として ブラック・ショールズ式などが活用されます。たとえばコールオプション(ヨーロピアン・コールオプション)の価値は ブラック・ショールズ式で理論的に計算することができます。
数式の中のSが株価、μはドリフト係数、rは無リスク金利、σはボラティリティ、Cがコールオプションの価値、kが権利行使価格です。また、dWは確率過程(ウィナー過程)、N()が正規分布の累積分布、eがネイピア数を表しています。ここまでは基礎編と同じ仮定を置いています。
基本の式では、現在の価格(S0)と満期時の価格(St)のみを使いますが、今回は任意の時間ステップで成立する 離散化式を利用します。

ノックアウト・オプションの表現と導入
ノックアウトをExcel上で再現する
今回の例では、以下のステップでモデル構築を行い、モンテカルロ・シミュレーションによって オプション価値を算定してみました。
- 株価の変動モデルを作成する
- ノックアウト・オプションの判定モデルを追加する
- 満期時の株価と権利行使価格の差(ペイオフ)を計算する
- ペイオフの期待値を現在価値に割戻して、オプション価値を算定する
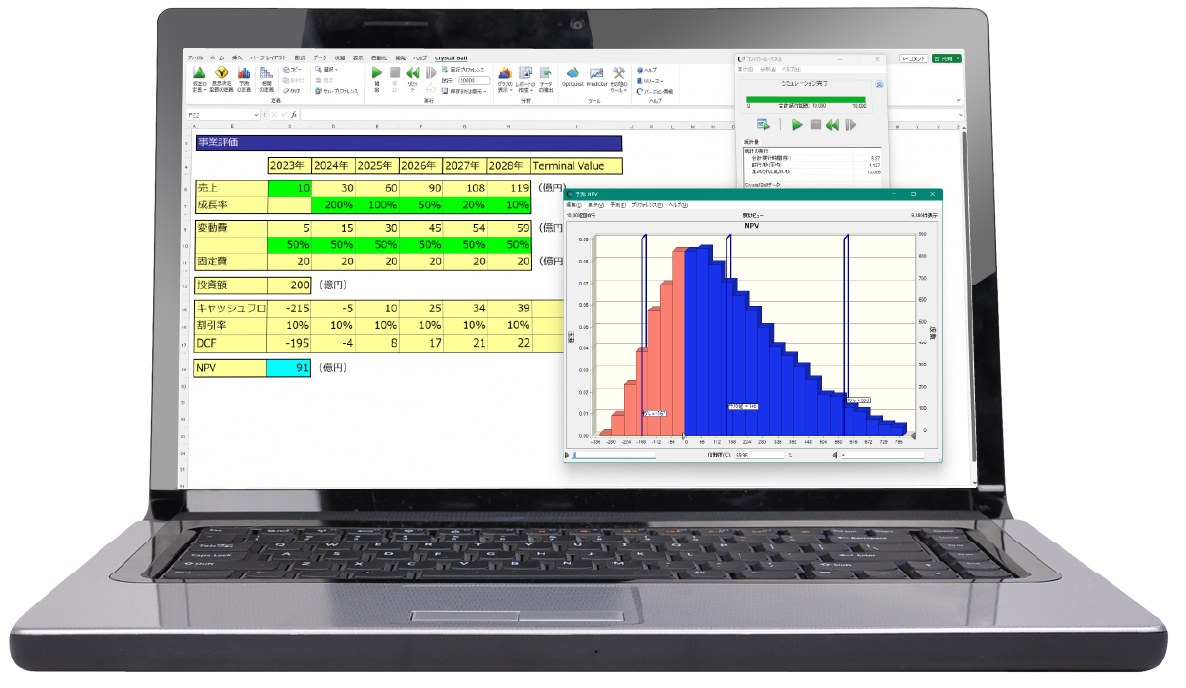
ExcelとCrystal Ballを用いると、以下のような表現が可能です。使用している仮定は標準正規分布です。また、ペイオフの期待値を取得するために、Crystal Ballのワークシート関数「CB.GetForeStatFN(ペイオフ,2)」を使用しました。最初の状態はエラーですが、Crystal Ballのシミュレーションを実行することで値が入ります。
シミュレーションモデルを作成する場合は、金利やボラティリティーなどのパラメータを入力する欄と 時間ごとの株価推移などを計算する表を分けて作成すると分かりやすくなります。
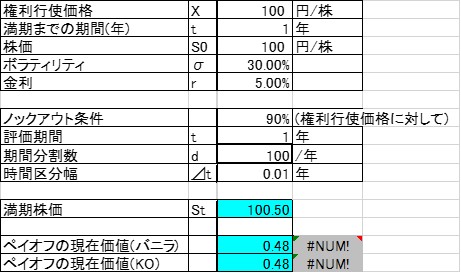
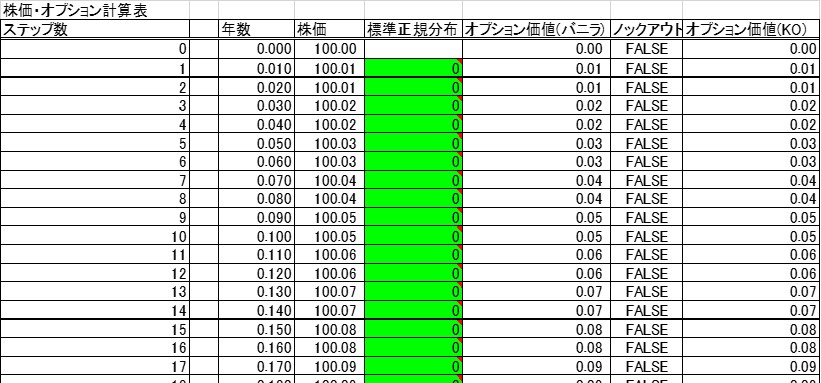
シミュレーションの結果
満期時点での株価とペイオフの現在価値をシミュレーションした結果を記載していきます。 まずは株価。様々なところで言われている通りの対数正規分布の形になっています。
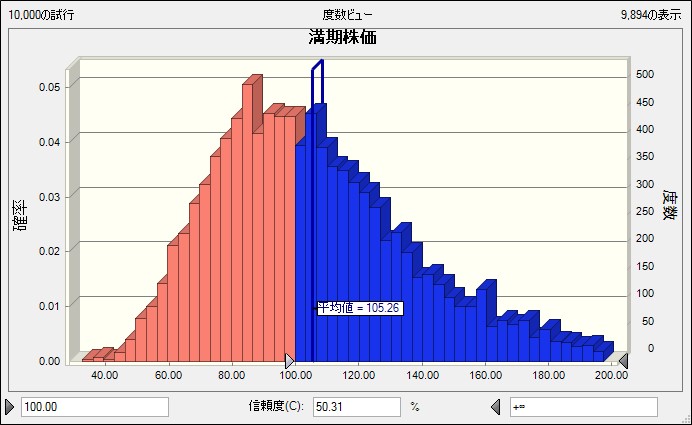
モンテカルロ・シミュレーションを利用した場合は、「ペイオフの現在価値の平均値」がオプション価値になります。今回はノックアウト条件を付けたため、時間軸の分割数(期間分割数d)を1, 10, 100の3パターンで計算してみました。
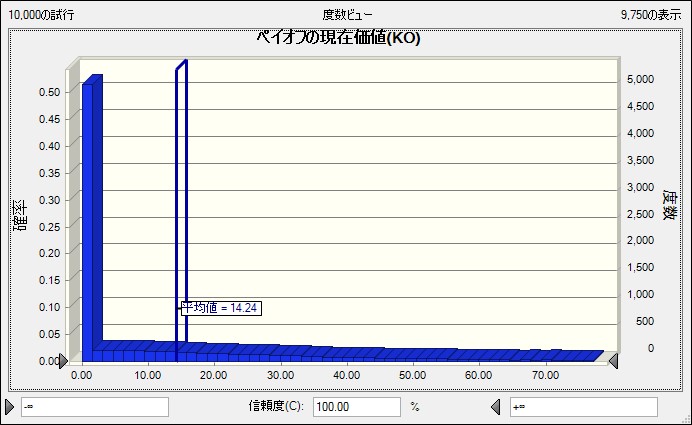
期間分割数 d=1 の場合
d = 1 の場合 平均値は「14.24」となりました。こういった計算だと、株価が下がって権利を放棄する場合が含まれるため 価値が0となるケースが一定割合含まれていることが分かります。
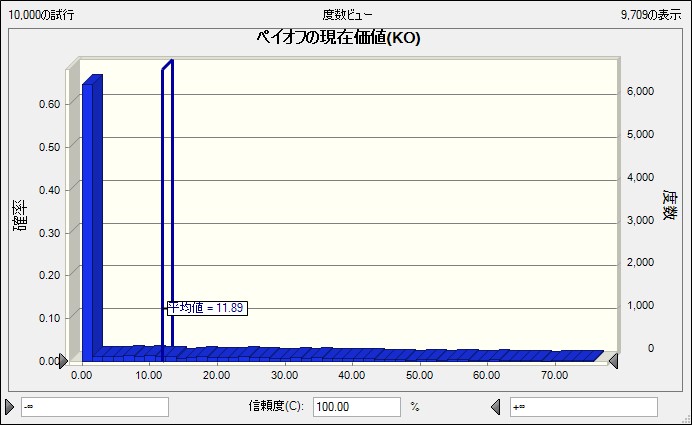
期間分割数 d=10 の場合
平均値は「11.89」となりました。d = 1 の場合と比べて平均値が小さくなっています。
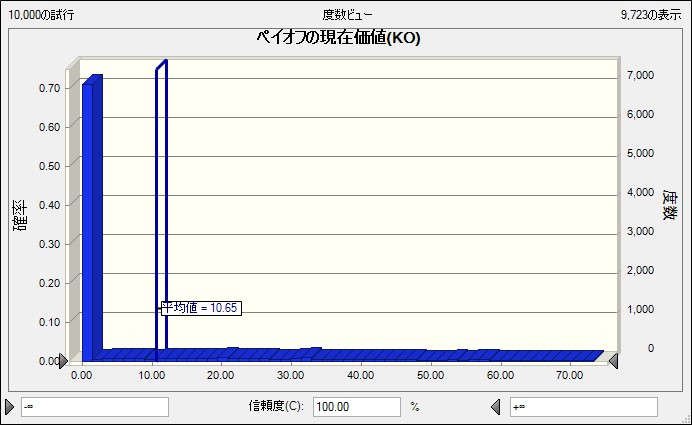
期間分割数 d=100 の場合
平均値は「10.65」となりました。さらに平均値が小さくなっています。
分割数を増やすほど、オプション価値が下がってしまうのは何故でしょうか?
理由としては、今回追加したノックアウト条件が原因です。「分割数を増やす → ノックアウトの判定回数が増える → ノックアウトしやすくなる」 という理由になっています。この方法で理論値を得るには無限大の分割数が必要となるわけですが、残念ながらそれは無理なのでどの程度の分割数とすれば良いのかを別途考えておく必要があります。たとえば今回はストックオプションということで、株が対象となっているため 1週間に1回判定とする前提なら分割数は50くらいかなと考えられますし、毎日の終値で判定とするなら分割数は250くらいになるかと思います。
活用してみよう!
基礎編・応用編と合わせて2つの記事で、Crystal Ball を活用したモンテカルロ・シミュレーションによるストックオプションの公正価値算定をご紹介しました。今後、複雑化していくであろう条件付けにも Excelワーク次第で対応していくことが可能かと思われます。
今回利用したサンプルファイルは無料でお配りしております。また、シミュレーションを実行するために必要となるCrystal Ball も15日間の無料体験期間がございます。サンプルファイルとCrystal Ball (無料体験)は、いずれも以下のリンクからダウンロード可能です。今回指定した株価やボラティリティなどの数値を変更してシミュレーションしてみることが可能です。ぜひお手元でお試しください。
また、詳細の説明やデモに興味がある、こんなケースでも利用できるか確認したい、という場合には、ぜひ担当者までお問い合わせ(リンク)ください。
サンプルファイルのダウンロード
弊社の個人情報に関する取り扱いについては「個人情報の取り扱いについて」(プライバシーマーク付与認定済)をご覧ください。
